Sophism #20: The Braess's Paradox

Sophisms are closely related to paradoxes. Both assume the form of a statement that contradicts your intuition. In case of a sophism, your intuition is right in telling you that the statement is wrong and its proof is simply flawed somewhere (yet it may not be obvious where exactly). In a paradox it is the other way around: the statement is valid, but simply unintuitive. In both cases, however, you learn something by reflecting on the statement or its proof, be it a subtle mathematical trick or a strange way in which the world actually works. Although paradoxes could probably deserve a whole series of their own, let us mix them into this "Sophisms" list for the sake of variety.

The New Airport

A new airport has been just built near the (imaginary) city of Springfield.

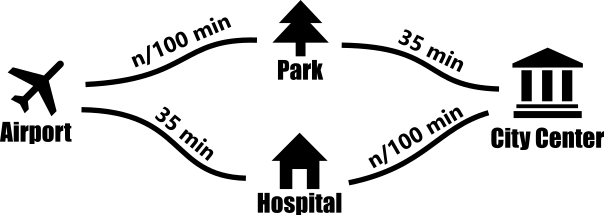
Two different roads lead from the airport to the city center - one crosses the park, and another passes near the city hospital. The road between the airport and the park is short, but gets quickly crowded with traffic jams. It has been estimated that when n cars are using the road, it takes about n/100 minutes for each of them to reach the park. The same holds for the road going from the hospital downtown.

The highways between the airport and the hospital and between the park and the city center are long, but wide - both are a 35 minute-long drive no matter how many cars are using them.

Every day 3000 cars need to get from the airport to the city. Assuming the car drivers have sufficient information about potential traffic jams on the road and try to behave in a selfishly optimal manner, it is not hard to see that they would split approximately equally between the two routes. This way each car would reach the city center in 1500/100 + 35 = 50 minutes.

Optimizing Traffic

Mr. O'Donnell, the mayor of Springfield, travels often and would like to improve the time it takes for him to get to the airport. He consulted his city planning specialists, who noted that the Park and the Hospital are quite close to each other: a shortcut road could be built between the two, which would only take a couple of minutes to traverse. As the "shorter" roads (Airport - Park, and Hospital - City center) only take 15 minutes to traverse at the moment, with the introduction of the new shortcut there would be a way to reach the city from the airport by passing both park and hospital in just 15+2+15=32 minutes, right?

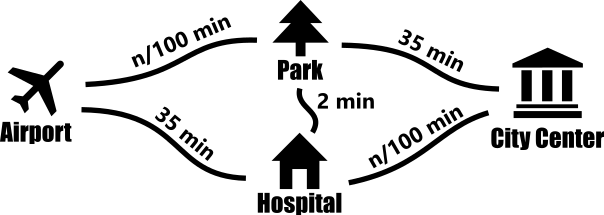
As soon as the new shortcut road was opened, something unexpected happened, however. All the drivers who previously took a long, 35-minute highway, would now switch to the shorter, traffic-jammed alternative. The highways somehow just made no sense any more. Even with all 3000 cars crammed onto the shorter road, the 32-minute Airport-Park-Hospital route would still always be preferable to the 35-minute Airport-Hospital highway. Similarly, the Park-Hospital-City road was preferable to Park-City highway at all times. Consequently, the next time Mr. O'Donnell drove from the airport to the city center it took him 30+2+30=62 minutes!

The Price of Anarchy

This situation is known as the Braess's paradox, named after the German mathematician who first took note of it. It is not just a mathematical curiosity - examples of it can be observed in reality as well. Citing the Wikipedia article, for example:

• In Seoul, South Korea, a speeding up in traffic around the city was seen when a motorway was removed as part of the Cheonggyecheon restoration project.
• In Stuttgart, Germany, after investments into the road network in 1969, the traffic situation did not improve until a section of newly built road was closed for traffic again.
• In 1990 the temporary closing of 42nd Street in New York City for Earth Day reduced the amount of congestion in the area.
• In 2008 Youn, Gastner and Jeong demonstrated specific routes in Boston, New York City and London where that might actually occur and pointed out roads that could be closed to reduce predicted travel times.
• In 2009, New York experimented with closures of Broadway at Times Square and Herald Square, which resulted in improved traffic flow and permanent pedestrian plazas.

The reason for the paradox lies in the unfortunate negative impact of uncoordinated selfish behaviour. It turns out that the lack of the shortcut road in the original road network was key to limiting the choices for the selfish drivers. This limitation was implicitly forcing them to cooperate and share the otherwise "inefficient" highway segments, which was beneficial for the system as a whole and for all its participants.

The inefficiency brought into the system by selfish behaviour is. of course, not limited to just cars on the road. It is a much wider phenomenon, generally known as "the price of anarchy". It is a source of many other paradoxes, which will be mentioned in some of the later posts of this series.

---

For other sophisms check out my other post.