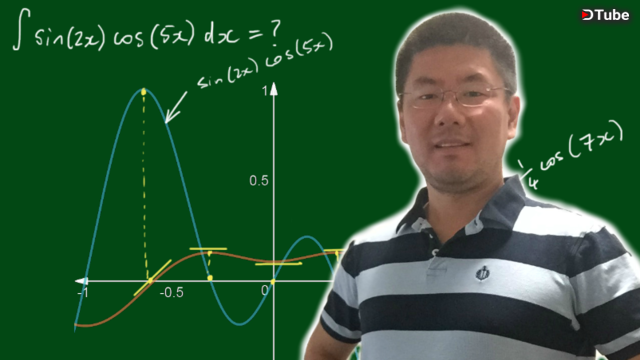
In this video, we work through the integral of ∫sin(2x)cos(5x)dx. The first step when performing any integral is to see if we can simplify the integrand, which in this case is:
sin(2x)cos(5x)
Luckily, we can do this with a trigonometric identity called the product to sum formula:
sin(u)cos(v) = 1/2[sin(u+v) + sin(u-v)]
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
I would really appreciate any small donation which will help me to help more math students of the world. Please donate here: https://paypal.me/MasterWu
▶️ DTube
▶️ IPFS
Great to see your post but way above my head.
Thanks @stephen-somers. Hope to catch up with you and @frobear soon.
That’d be great. Maybe time for another SEQ Steemup.
I will ask my teacher about this tomorrow
Thanks @frobear. I'd love to hear your teacher's feedback!
Yuhh sometimes it is really need to refresh how solve such tasks. Thank you for this short video.
Posted using Partiko Android
Congratulations @masterwu! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @masterwu! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Congratulations @masterwu! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!