
For the English version see here.
Hi Leute,
es ist schon eine Weile her, dass ich etwas in dieser Reihe geschrieben habe. Dennoch hoffe ich, dass ihr euch über einen weiteren Teil der Serie freut, der auch sicher nicht der Letzte sein wird. Da der Artikel etwas länger geworden ist, habe ich die deutsche und englische Version getrennt. Das Thema ist ein bisschen komplizierter, aber ich hoffe, dass ihr trotzdem mitkommt.
Heutiges Thema
Heute geht es um die Themen „Pyro- und Piezoelektrizität“. Einige von euch werden jetzt vielleicht denken: „Was? Was soll das sein? Wie spricht man das aus? Und was hat das mit meinem Alltag zu tun?“ Nun, diesen Fragen wollen wir uns im Folgenden widmen:
Bedeutung der Begriffe
Unter Elektrizität kann sich wohl jeder von euch etwas vorstellen. Tatsächlich haben beide Begriffe etwas mit elektrischem Strom zu tun. Die Vorsilben pyro und piezo kommen aus dem Griechischen und sind ein Verweis auf Feuer (man kennt z.B. auch Pyrotechnik) bzw. auf drücken. Unsere beiden Begriffe haben also mit einer Eigenschaft zu tun, die Elektrizität in Verbindung mit Wärme bzw. einer mechanischen Verformung bringt. Wie es dazu kommt und wozu man diese Eigenschaften verwenden kann, sehen wir nach ein paar kurzen Erläuterungen zum Thema Symmetrie.
Exkurs: Symmetrie in Kristallen
Das Thema wäre sicherlich Stoff für einen ganzen Artikel, daher hier nur kurz ein paar Anmerkungen zum besseren Verständnis der folgenden Abschnitte.
So genannte Symmetrieoperationen führen dazu, dass ein Objekt nach der Durchführung der Operation wieder genauso erscheint, wie es vor der Operation war. Durchführen kann man sie an Symmetrieelementen.
Ein Beispiel ist eine Drehung, die um einen bestimmten Winkel ausgeführt wird. Das zugehörige Symmetrieelement ist eine Drehachse. Stellen wir uns einen Würfel vor, der auf jeder Seite einen Punkt (für die Zahl 1) hat. Wenn man diesen einmal um 360° dreht, sieht er identisch aus wie vorher und erfüllt daher unser Kriterium. Das ist einsichtig und eine Symmetrieoperation, die mit jedem Objekt möglich ist.
Legen wir unsere Drehachse genau durch die 1 unseres Würfels sind außerdem weitere Operationen möglich: Die Drehung um 360/2 = 180° führt ebenfalls zu einem vom Ursprung nicht unterscheidbaren Bild (vorausgesetzt, der Würfel hat keine Kerben oder ähnliches). Nach zweimaliger Drehung befindet sich das Objekt wieder im Ausgangszustand. Wichtig dabei ist, dass aber eben auch die halbe Drehung schon zu einem äußerlich identischen Zustand führt. Daher ist diese Drehung nicht mit jedem beliebigen Objekt möglich. Ist diese Art der Drehung möglich, spricht man von einer zweizähligen Drehachse.
Die letzte Möglichkeit, den Würfel zu drehen, ist eine Drehung um 360/4 = 90°. Hier gilt sinngemäß dasselbe wie für die zweizählige Achse: Nach jeder Vierteldrehung haben wir ein äußerlich identisches Objekt und nach vier Drehungen den ursprünglichen Zustand. Diese vierzählige Achse enthält folglich auch immer eine zweizählige sowie eine einzählige Achse.
Weitere Drehungen, die obiges Kriterium erfüllen, sind mit dem Würfel in dieser Position nicht möglich. Eine Drehung um z.B. 360/3 = 120° (eine dreizählige Achse) würde man sofort sehen können.
Neben den Drehachsen gibt es beispielsweise Spiegelebenen, die die rechte Hälfte eines Objekts auf der Linken abbilden und umgekehrt (oder vorne auf hinten bzw. oben auf unten). Es gibt auch kombinierte Symmetrieelemente, wie beispielsweise eine Schraubenachse oder Drehinversion, die allerdings für uns im Moment nicht relevant sind.
Auftreten der Eigenschaften
Beide Eigenschaften können vor allem in Kristallen von bestimmten Mineralien/Salzen auftreten, die allerdings einen besonderen Aufbau (genauer: eine besondere Symmetrie) haben müssen. Das heißt in diesem Zusammenhang, dass beispielsweise bestimmte Spiegelebenen nicht vorhanden sein dürfen. Da die Struktur hier die Eigenschaften bedingt, spricht man auch von Struktur-Eigenschafts-Beziehungen.
Wie ihr z.B. hier in einem früheren Artikel nachlesen könnt, bestehen Salze aus Anionen und Kationen, also negativen und positiven Teilchen. Deren Anordnung ist wichtig für die hier diskutierten Eigenschaften (andere Möglichkeiten, um diese hervorzurufen, sind polare Moleküle, die z.B. hier erklärt werden).
Ich möchte versuchen, euch die beiden Eigenschaften anhand der Verbindung Zinksulfid (ZnS) zu erläutern. Obwohl diese immer aus gleich vielen Zink- und Schwefelatomen (bzw. -ionen) besteht, gibt es zwei Arten von Zinksulfid. Diese Varianten (so genannte Modifikationen) unterscheiden sich darin, wie die Atome sich zusammenlagern. Man unterscheidet die beiden natürlich vorkommenden Mineralien Sphalerit (auch Zinkblende) und Wurtzit. Sphalerit ist dabei eine kubische Variante (hat also eine ähnliche Symmetrie wie ein Würfel) und Wurtzit ist hexagonal (hat also eine sechszählige Symmetrie).
Wurtzit und die Pyroelektrizität
Schaut man sich die so genannte Einheitszelle (das ist die kleinste Baueinheit einer ionischen Verbindung, aus der man die gesamte Struktur erhält, wenn man sie immer wieder neben- und übereinander stapelt) von Wurtzit an, so fällt auf, dass es eine Abfolge von Schichten gibt, wobei immer ein etwas längerer und ein etwas kürzerer Abstand zu finden ist. Man hat – von der Seite aus gesehen – also einen Aufbau der Art S-Zn – S-Zn – S-Zn und so weiter.
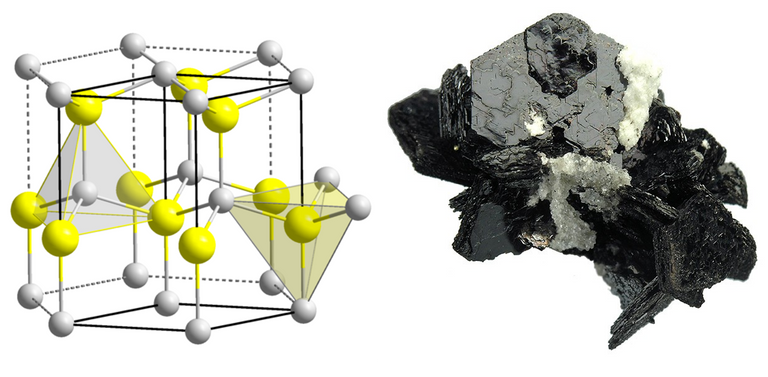
links: Bild der Einheitszelle (Schwefel gelb, Zink grau), rechts: Bild des Minerals.
Quelle: Struktur, Mineral
Dieser schichtartige Aufbau, den man auch makroskopisch, d.h. bei sichtbar großen Kristallen, erkennen kann (siehe Bild) hat zwei Eigenschaften zur Folge:
- Das Material blättert leicht ab (wie z.B. auch Schiefer).
- Wurtzit ist pyroelektrisch.
Wie kommt es nun zur Pyroelektrizität und was genau heißt das? Schwefel liegt in unserer Verbindung als Anion S2- vor und Zink als Kation Zn2+. Das hat zur Folge, dass jeder der Ionenschichten eine positive und eine negative Seite hat. Da es insgesamt gleich viele Schichten von beiden Sorten gibt, ist das Mineral als Ganzes elektrisch neutral. Wir können also die oben genannte Schichtfolge auch in der Form +- +- +- etc. darstellen. So fällt auf, dass auch im großen Ganzen eine negative und eine positive Seite vorhanden ist. Das Mineral ist daher ein großer elektrischer Dipol, der prinzipiell entsprechend kontaktiert und gemessen werden kann.
Wenn sich die Temperatur ändert, dehnt sich das Mineral aus bzw. zieht sich zusammen, weil die Ionen sich stärker bzw. schwächer bewegen (siehe auch hier). In der Folge ändert sich die Stärke des Dipols und damit das Messsignal. Dieser Effekt wird als Pyroelektrizität bezeichnet.
Sphalerit und die Piezoelektrizität
Auch die Einheitszelle von Sphalerit hat einen besonderen Aufbau, den man hoffentlich anhand des Bildes erahnen kann: Stellt man sich einen größeren Würfel vor, der aus acht kleineren Würfeln aufgebaut ist, kann man sehen, dass jeweils zwei der kleineren Würfel pro Ebene ein Schwefelion enthalten und die beiden anderen nicht. Die gefüllten Würfel sind versetzt angeordnet.
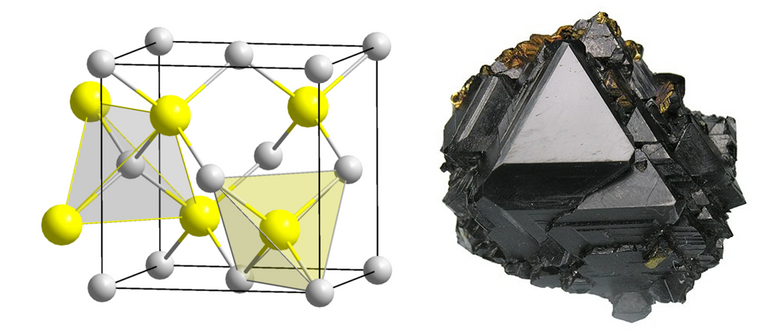
links: Bild der Einheitszelle (Schwefel gelb, Zink grau), rechts: Bild des Minerals.
Quelle: Struktur, Mineral
In der oberen Schicht sind z.B. der vordere linke und hintere rechte Würfel und in der unteren Schicht der vordere rechte und hintere linke Würfel gefüllt (man kann auch nach vorne-hinten oder rechts-links schauen und findet immer das abwechselnde Muster). Die Zinkionen dagegen sind über den gesamten Würfel gleichmäßig verteilt, nämlich in allen Ecken und den Flächenmitten (wie ein Würfel, der sechsmal die 1 trägt).
Die negative Ladung des Schwefels ist durch die Struktur also nur in vier der acht Ecken verteilt. Die Vektoren der Dipole, also deren Richtungen, zeigen ebenfalls in diese vier Ecken. Dennoch sind sie so symmetrisch angeordnet (wer es wissen will: durch eine Drehinversion/-spiegelung), dass sie sich gegenseitig genau aufheben. Vereinfacht gesagt sind aus jeder möglichen Blickrichtung gleich viele Dipole in und gegen die Richtung zu sehen.
Wenn auf den Kristall ein Druck ausgeübt wird, verformt sich die Zelle z.B. so, dass eine Seite kürzer ist, als die anderen. Dadurch verschwindet die vierzählige Drehachse und eine zweizählige bleibt zurück. Gleichzeitig sind auch die Dipole nicht mehr gleichmäßig verteilt und heben sich nicht mehr in allen Richtungen gegenseitig auf. In der Folge kommt es wiederum zur Ausbildung einer positiven und negativen Seite der Zelle bzw. des Kristalls, die ebenfalls messbar ist. Dieses Phänomen heißt Piezoelektrizität. Umgekehrt ist es bei piezoelektrischen Materialien auch möglich, eine äußere Spannung anzulegen, die dann zu einer Verformung des Materials führt.
Pyro- und Piezoelektrizität im Alltag
Die beiden Phänomene mögen exotisch erscheinen, sind aber tatsächlich gar nicht so selten anzutreffen. Da pyroelektrische Materialen im Prinzip einen Zusammenhang zwischen Wärme und elektrischer Spannung schaffen, sind sie grundsätzlich geeignet, um als Temperatursensoren zu dienen. Weiterhin können sie beispielsweise in Bewegungsmeldern eingesetzt werden, die auf der Erfassung von Wärme beruhen.
Häufiger findet man allerdings piezoelektrische Bauteile. Diese kommen z.B. als Zünder in elektrischen Feuerzeugen oder als Tonabnehmer auf E-Gitarre oder -Bass zum Einsatz. Auch der Schwingquarz in Uhren beruht auf dem Prinzip der Piezoelektrizität. Den umgekehrten Weg, durch Elektrizität eine Verformung hervorzurufen, kann man z.B. für Stellmotoren in hochpräzisen Geräten einsetzen. Ebenfalls beruhen einige Lautsprecher (z.B. in Kopfhörern) auf der Piezoelektrizität.
Zum Abschluss
Ich hoffe, ich konnte euch die Thematik grundsätzlich erläutern. Für weitere Informationen verlinke ich euch wieder die Wikipedia-Artikel. Für Fragen und Anregungen nutzt bitte gerne die Kommentare.
Bis zum nächsten Mal!
Weitere Informationen
[Symmetrie](https://de.wikipedia.org/wiki/Symmetrie_(Geometrie)
Pyroelektrizität
Piezoelektrizität
Schwingquarz
Ferroelektrischer Lautsprecher
Sehr schön und anschaulich erklärt.
Hallo;)
Anschaulich erklärt? Ich bin der Meinung, er sollte ein Lehrer an unseren Schulen sein!!! Das würden die Schüler interessieren, weil sie es verstehen und etwas damit anfangen könnten. Hut ab!!! Die einfachsten Sachen sind die Besten.
Ich war jetzt nicht der Meinung, dass gerade dieses Thema soooo gut erklärt war, weil es eigentlich recht komplex ist, aber freut mich, wenn du das anders siehst. Vielen Dank! :-)
Werde Lehrer, du Genie ;)
Danke!
Freut mich besonders wieder etwas von dir hier zu sehen! Ich hatte übrigens eine ähnliche Idee zu einer Beitragsreihe "know your physics" oder wie du es beschreibst, Wissenschaft im Alltag 😀
Dankeschön! Tu dir keinen Zwang an. Ich hab zwar auch noch ein paar Themen auf dem Zettel, aber selbst wenn wir über das selbe schreiben würden, hätten wir ja sicherlich verschiedene Aspekte. Von daher: Hau in die Tasten, ich warte schon mit dem Upvote auf dich! ;-)
Very interesting post..nice to know you @thepe.