In meinem Artikel Ein chaotisches Wettermodell im Insightmaker haben wir ein (etwas primitives) Modell eines komplexen, weil chaotischen Systems entwickelt und konnten ein verschwommenes Bild eines seltsamen Attraktors erhalten. Es hat uns aber genügt, um den Begriff "Komplexität" zu verstehen: die Dynamik des Systems folgt einer nicht in sich geschlossenen, unendlich in sich verschlungenen Bahn in einem begrenzten Gebiet eines möglicherweise hochdimensionalen Raumes.
Offenbar liessen sich einige Leser durch den Titel täuschen. Es ging natürlich nicht um Wettermodelle, sondern um ein (einfaches) Beispiel eines komplexen Systems, an dessen Dynamik wir "Komplexität" studieren wollten.
Die Dimensionen eines komplexen Systems
Die Dimensionen des Raums sind die Parameter, mit denen wir uns auseinander setzen müssen. In unserem einfachen Wettermodell hiessen die Dimensionen X, Y und Z und haben etwas komplizierte Entsprechungen in der Realität. X entspricht der zirkulären Geschwindigkeit eines Flüssigkeitspakets in einer Konvektionszelle. Y entspricht der Temperaturdifferenz zwischen einem aufsteigenden und einem benachbarten abfallenden Flüssigkeitspaket auf einer bestimmten Höhe. Z schliesslich misst die Abweichung vom linearen Temperaturgefälle zwischen der unteren und der oberen Begrenzung der Flüssigkeitsschicht.
Übertragen auf ein viel komplexeres soziales System, wie z.B. ein Unternehmen, gibt es viel mehr Parameter: Zuverlässigkeit der Lieferanten, Zuverlässigkeit der Technologien, Konkurrenz, Markt, Geschmack der Kunden, Mode, Mitarbeiter, Motivation, Kulturen, Überzeugungen, Befürchtungen, Erwartungen, etc. Einige können "Materialeigenschaften" sein, wie im Wettermodell Dichte oder Viskosität, andere können "Kontrollparameter" sein, wie die Temperatur der Heizplatte im Bénard-Versuch und wieder andere können in Kombination die Dimensionen des Phasenraums ausmachen, in dem sich das System "Unternehmen" bewegt. Der Phasenraum eines Unternehmens ist also hochdimensional und sehr abstrakt. Entsprechend verflochten kann die Bahn sein, die die Entwicklung des Unternehmens abbildet.
Drei Arten von Attraktoren
Ein Punkt im Phasenraum bewegt sich auf einer Bahn, die vielleicht einmal in einem begrenzten Gebiet bleibt. Das entspricht dem Alltag in einem sozialen System. Das Büro ist immer dasselbe, das Team, die Kunden und Zulieferer bestehen über lange Zeit aus denselben Personen, mit denen wir uns täglich auseinandersetzen, die Mittel und Methoden bleiben ebenfalls lange dieselben, bis die Entscheidung getroffen wird, etwas zu verändern. Die Art der Entscheidung und die Art, wie Methoden und Mittel verändert werden, bleibt gleich. Prozesse bleiben über lange Zeit dieselben, bis auch hier entschieden wird, neue Prozesse einzuführen. Die neuen Prozesse werden in einer dem Unternehmen eigene Art designt und eingeführt, etc. Zwar "bewegt" sich stets etwas im Kleinen, aber im Grossen und Ganzen kennen wir das System. Wir bleiben also mit der Unternehmensdynamik in einem begrenzten Gebiet gefangen. Man spricht in diesem Falle von einem Attraktor. Ein Attraktor ist ein begrenztes Gebiet des Phasenraums, in dem die Systemdynamik für alle Zeiten gefangen bleibt. Ich kann mir aber vorstellen, dass sich dieses Gebiet selber auch verschieben kann, so dass dennoch alles möglich bleibt.
Es gibt nun im Prinzip drei verschiedene Attraktoren:
Der Punktattraktor
Die Bewegung des Systems kommt zum Stillstand. Wir kennen das von einem Pendel: ein Massepunkt ist mit einem Drehpunkt über eine masselose starre Stange verbunden. Wenn wir das Pendel ein wenig auslenken, dann beginnt es zu schwingen, also hin- und herzupendeln. Der Drehpunkt ist i.A. nicht reibungsfrei und bremst das Pendel ab. Es schwingt möglicherweise lange hin- und her, aber die Auslenkung nimmt jedesmal um einen kleinen Betrag ab, bis das Pendel schlaff nach unten hängt und zum Stillstand gekommen ist. Die Bahn dieser Dynamik, entspricht einer immer enger werdenden Spirale. Der Ruhezustand ist der Punkt im Zentrum der Spirale. Das ist der Grenzpunkt, an dem das Pendel zur Ruhe kommt.
Ein System, dessen Entwicklung an einem bestimmten Punkt stillsteht, können wir als totes System bezeichnen.
Grenzzyklus und Knotenattraktoren
Angenommen nun, der Drehpunkt wäre reibungsfrei, oder - was auf dasselbe herauskommt - wir stossen das Pendel jedesmal gerade mit denjenigen Impuls an, der der Energie entspricht, die während der letzten Schwingung im Drehpunkt dissipiert wurde. Die Dynamik des Systems entspricht also völliger Routine, in der sie den Weg zwischen den beiden Umkehrpunkten immer wieder durchläuft. Wenn wir das Pendel also ein wenig auslenken, dann schwingt es ewig hin- und her. Es durchläuft ständig dieselbe Bahn. So etwas nennt man Grenzzyklus.
So sieht ein Grenzzyklus aus: Die Entwicklung der Systemdynamik nähert sich dem Grenzzyklus und bewegt sich dann für ewige Zeiten darauf.

Ein System, dessen Entwicklung ständig zwischen zwei Umkehrpunkten hin- und her schwingt, können wir als einfaches System bezeichnen.
Ein Grenzzyklus muss nicht immer ein idealer Kreis sein. Die Systemdynamik kann sich auf einem hochkompliziert verschlungenen Knoten bewegen. Sie durchläuft weite Teile des Phasenraums, bis sie wieder exakt zum Ausgangspunkt zurückkehrt. Dann fängt die exakt gleiche Reise erneut an. Es kann auch sein, dass sich die Systementwicklung auf die Bahn zu bewegt, die einem mehr oder weniger verschlungenen Knoten gleicht und sich dann für ewige Zeiten darauf bewegt.
Hier zwei mögliche solche Knotenattraktoren:

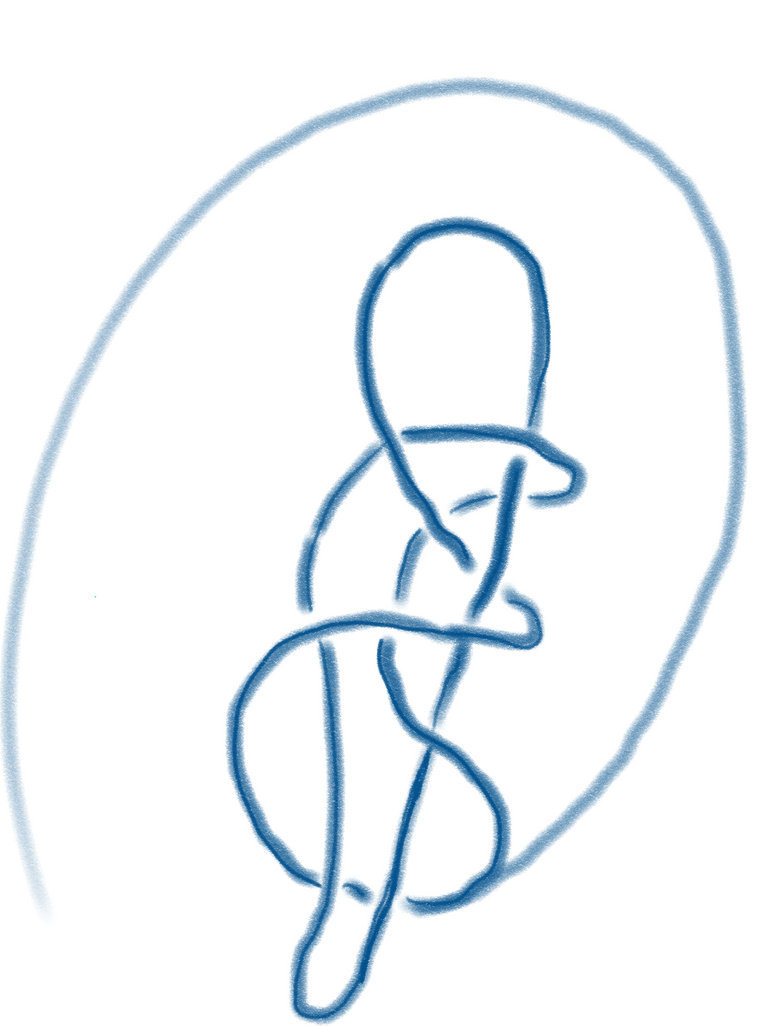
Ein solches System können wir als kompliziertes System bezeichnen.
Seltsame Attraktoren
Der Knoten kann im Extremfall eines Seltsamen Attraktors "unendlich verschlungen" sein. Das bedeutet, dass die Systemdynamik nie wieder zu einem Ausgangspunkt zurückkehrt. Der "unendlich verschlungene Knoten" auf dem sich die Systemdynamik bewegt, ist völlig chaotisch. Solche Systeme sind Komplexe Systeme.
Das ist schon bei einem Bénard- oder Wettersystem der Fall. Es gibt nie zwei exakt gleiche Wettersituationen. Es mag sein, dass heute Mittag eine Wettersituation herrscht, die stark der Wettersituation gleicht, wie sie am 25. September 1756 um 13 Uhr herrschte. Aber exakt gleich sind die beiden ganz sicher nicht. Und vor allem entwickelten sie sich ganz verschieden. Das bedeutet, dass die beiden Wettersituationen, die sich gleichen, ein paar Minuten später völlig verschieden sein können, so dass man nicht denken würde, dass die beiden Wettersituationen vor paar Minuten fast gleich waren.
Komplexe Systeme sind immer chaotisch!
Ein System, das in seiner Entwicklung in immer einer anderen Situation ist und sich seine Situation nie wiederholt, ist ein komplexes System.
Chaotisch bedeutet ja:
Die Entwicklung ist volatil. Sie kann tage- oder wochenlang vor sich hindümpeln, um dann plötzlich und ohne Vorankündigung eine grosse Veränderung zu erfahren.
Die Entwicklung ist zu keinem Zeitpunkt vorhersehbar. Es ist völlig ungewiss, ob sich ein Systemparameter in der näheren Zukunft verstärkt oder abschwächt.
Entwicklungseigenschaften können stets verschieden gedeutet werden. Letztes Jahr um diese Zeit krähte der Hahn auf dem Mist und das Wetter blieb, wie es war. Heute krähte der Hahn auch wieder auf dem Mist und dennoch kommt es kurz darauf zu einem tollen Wetterumschwung. Eine chaotische Systementwicklung ist also stets mehrdeutig.
Diese drei (unter vielen) Eigenschaften komplexer Systeme fasst der Volksmund gemeinhin im Akronym VUCA - Volatility, Uncertainty, Complexity, Ambiguity - zusammen, wobei das C hier nicht hingehört, denn es ist Ursache der drei Eigenschaften. Aber es gibt noch viel mehr Eigenschaften komplexer Systeme, z.B. Emergenz, Verzögerungen, Verzweigungen, etc.
Eine andere Volkstümlichkeit, die diese Sachverhalte zusammenfassen will, ist die sog. Cynefin-Vierermatrix (Cynefin-Framework). Sie schiebt Systeme willkürlich in vier Schubladen: einfach, kompliziert, komplex und chaotisch. Ein wenig erinnert diese Klassifikation an unsere drei Attraktoren: Punkt, Grenzkreis und seltsamer Attraktor. Diese Einteilung ergibt sich aus der universellen Natur von Attraktoren, während die Cynefinmatrix völlig willkürlich ist und keine Grundlage hat. Zudem übersieht sie, dass komplex gerade chaotisch heisst. Beispielsweise ist der Herzschlag chaotisch und damit ist das System Herz komplex. Ein Herz, dessen Herzschlag stets exakt gleich ist, also bloss kompliziert, ist krank.
Wir können daraus etwas für den Umgang mit komplexen Systemen lernen:
Nur komplexe Systeme sind zur Innovation fähig. Je komplexer, desto innovativer kann es sein.
Nur in einem komplexen System sind wirkliche Veränderungen möglich. Je komplexer, desto mehr Veränderungen kommen vor.
Ein komplexes System ist immer chaotisch, d.h. volatil, ungewiss, mehrdeutig, etc.
In einem komplexen System erfolgreich zu handeln gelingt nur denjenigen Personen,
⦁ die offen für Andersartiges und Neues sind, d.h. flexibel auf Veränderungen reagieren,
⦁ die neugierig sind, viel fragen und furchtlos immer wieder Neues ausprobieren,
⦁ die sensibel sind auf sich bietende Gelegenheiten.
Super. Resteem. Bin jedoch etwas verwirrt
Wenn ein (natürliches) System in seinem Verhalten einen seltsamen Attraktor generiert oder seine Dynamik ihm zu folgen scheint, dann ist dieses "chaotische" Verhalten eine Emergenz aus der Komplexität.
Komplexität ist wiederum eine Emergenz aus der Entropie. In der Informationstheorie ist der komplexeste String (als 1-dimensionales System), jener mit der höchsten Entropie/ "Unordnung"
Je nach Betrachtungsweise (systemtheoretisch, informationstheoretisch, mathematisch) meint Entropie, Rauschen, Zufall doch das selbe? *gemessen an dem was tatsächlich IST.
Wenn Systeme als Generatoren modelliert/sich vorgestellt werden, meinetwegen unser Universum als Wellenfunktionsgenerator - sagen wir das IFS ist (M): z=z² +c (*nicht dass es so wäre aber nur mal angenommen, da das generierte System ein offenes geschlossenes System unendlicher Komplexität ist),
dann ist doch alles was ist, (aufgrund der mathematischen Funktionsweise): Die Veränderung, generiert durch den Iterationsprozess.
UND durch das hohe n bzw. statistische Gesetz der Zunahme der Entropie (aus welcher z.B. unsere Zeit emergiert), --> wächst die Unordnung. Elementar ist also nur und allein die Veränderung und der Zuwachs an Unordnung (sofern man beobachtet). Sofern man nicht beobachtet ist allein die Iteration.
Dass determinstisch-chaotische Systeme selbst Zufall aka. Rauschen aka. Unordnung generieren, schließt ja nicht aus, dass sie selbst aus dem Zufall heraus emergieren.
Bei der Volatilität sehe ich z.B. mehr als nur Ungewissheit. Es hat etwas mit Exposition eines konkreten oder Referenz- Systems gegen über einer Quelle zu tun. Ereignisse hohen Sigmas haben dabei starke Auswirkungen auf das expositionierte System. Führen somit je nach Abweichung zur Bifurkation/Phasetransition im System. Beispiel: Das Wasser welches kocht. ...Ohne die Volatilität der Strahlenquelle nicht denkbar. Ist Volatilität somit phänomenal nicht die Abweichung von einem referenz Zustand? Die Ungewissheit resultiert ja wieder nur aus dem approximations Problem oder der fat-tailedness einer (scheinbar) zugrunde liegenden Wahrscheinlichkeitsverteilung. Z.B. einer heavy-tailed wie der Cauchy-Verteilung.
Vielen Dank für diesen vermutlich interessanten Kommentar, aber jetzt bin ich "etwas verwirrt"... Dein Kommentar ist stellenweise etwas verwirrend geschrieben. Aber ich versuche einmal, nacheinander auf Deine Hinweise einzugehen:
Ich würde nicht sagen, dass ein System einen Attraktor "generiert". Es ist wie Deine Biographie: Diese generierst Du ja auch nicht. Zwar versuchst Du, sie zu beeinflussen, aber letztendlich passiert mit Dir viel, was Du eigentlich nicht beabsichtigt hattest. Zu jedem Zeitpunkt kannst Du auf Dein bisheriges Leben zurückschauen und sagen: das war mein bisheriges Leben oder mein bisheriger Lebensweg. Dein Lebensweg ist Deine Entwicklungslinie. Genauso ist der Attraktor die Entwicklungslinie eines Systems.
Chaotisches Verhalten ist keine Emergenz. Chaotisches Verhalten ist eine andere Ausdrucksweise für "Entwicklung auf einem seltsamen Attraktor". In gewisser Weise sind "seltsamer Attraktor" und "chaotisches Verhalten" Synonyme. Das war eigentlich die Hauptaussage meines Artikels. Und "Komplexität" ist eigentlich ein Unwort, weil niemand genau weiss, was Komplexität ist, bzw. weil es ganz viele verschiedene Definitionen gibt. Ich bezeichne ein System als komplex, wenn es sich auf einem seltsamen Attraktor entwickelt.
Komplexität ist jedenfalls auch keine Emergenz. Beim Aufbau von Komplexität wird Entropie erzeugt. Den Begriff der Entropie wollte ich diesmal nicht erwähnen, aber Du gibst mir die Idee, einmal einen Artikel über "Komplexität und Entropie" zu schreiben. Vielen Dank.
Dann folgen in Deinem Kommentar ein paar (vermutlich interessante) Überlegungen über Veränderung und Iteration. Aber die Überlegungen sind nicht sehr klar formuliert, so dass es für mich schwer ist, sie nachzuvollziehen. Du erwähnst die iterative Abbildung, die zum Apfelmännchen führt. Ja, das ist ein nettes Zahlenbeispiel. Aber um den Zusammenhang zu physikalischen und biologischen Systemen zu bilden, müsste man hier wohl etwas tiefer eintauchen. Auch das wäre vielleicht einmal einen Artikel wert.
Ich bin nicht einverstanden, dass deterministisches Chaos und Rauschen dasselbe sind, also kein "aka"! Rauschen ist indeterminiert. Eine bekannte Kritik meiner Sicht, wie ich sie in meinem Artikel darlegte, ist, dass ich von determiniertem Chaos rede, während das Leben doch gerade indeterminiert sei. Darauf erwidere ich jeweils, dass ich nicht hoffe, sein Leben sei bloss Rauschen. Lebende Systeme sind eben gerade determiniert chaotisch!
Unter Volatilität verstehe ich das plötzliche Überschwingen innerhalb des Attraktors. Hast Du schon einmal zugeschaut, wie ein Attraktor zustande kommt? Hast Du z.B. die Simulation meines Modells des Lorenzsystems laufen gelassen und dabei zugesehen, wie der Attraktor entsteht? Der bekannte Attraktor des Lorenzsystems besteht ja aus zwei "Augen" oder "Äste". Die Systemdynamik kann lange Zeit einer Trajektorie innerhalb eines Astes folgen, um dann plötzlich und unvorhergesehen in den anderen Ast zu springen. Das ist die Volatilität, die ich meine.
Und ja, die Volatilität wirkt sich unvorhergesehen aus. Aber unter Volatilität verstehe ich das plötzliche Zurücklegen eines grossen Weges innerhalb des Attraktors. Der Attraktor eines hochkomplexen sozialen Systems hat vermutlich noch viel mehr "Äste" und ist sehr verworren und verzweigt. Da kann es zu grossen Ausschlägen kommen. Aber Du verstehst unter "Volatilität" offenbar etwas anderes. Du sprichst von der "Volatilität der Strahlungsquelle". Ob Du lokale Temperaturdifferenzen der Heizplatte meinst, die im Bénard-System zu den bekannten Fluktuationen innerhalb der horizontalen Flüssigkeitsschicht führen, wie ich das in einem meiner früheren Artikel beschrieben habe, wo ich das Bénard-System vorstellte?
Dann sprichst Du von Sigma, ich denke, Du meinst die Standardabweichung, und erwähnst die Cauchy-Verteilung, obwohl gerade die Cauchy-Verteilung gar keine Standardabweichung hat. Vielleicht hältst Du Dich besser an die Paretoverteilung, die auch "heavy-tailed" ist und von Nassim Taleb in seinem Schwarzen Schwan empfohlen wird.
Vielen Dank dass du dir die Zeit genommen hast. Es ist schwer Dinge zu kommunizieren, wo doch die Begrifflichkeiten kaum eindeutig definiert sind. Vermutlich müsst ich mich da mathematisch ausdrücken.
Genau um den epistemologischen Zusammenhang ging es mir. Ich weis, dass wie es der Name sagt, dem Attraktor gefolgt wird, welcher dem System eigen sein soll (als Entwicklungslinie)
nur sehe ich das nicht, sonder viel mehr eine reflexive Struktur. Aber ich lasse erstmal den Meister sprechen und folge gespannt den Artikeln, und werde die Vergangen nochmal aufarbeiten.
Congratulations @paaddor! You received a personal award!
Click here to view your Board
Do not miss the last post from @steemitboard:
Congratulations @paaddor! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!