Setup
This guide was written in Python 3.6.
Python and Pip
If you haven't already, please download Python and Pip.
Introduction
In this tutorial set, we'll review the Naive Bayes Algorithm used in the field of machine learning. Naive Bayes works on Bayes Theorem of probability to predict the class of a given data point, and is extremely fast compared to other classification algorithms.
Because it works with an assumption of independence among predictors, the Naive Bayes model is easy to build and particularly useful for large datasets. Along with its simplicity, Naive Bayes is known to outperform even some of the most sophisticated classification methods.
This tutorial assumes you have prior programming experience in Python and probablility. While I will overview some of the priciples in probability, this tutorial is not intended to teach you these fundamental concepts. If you need some background on this material, please see my tutorial here.
Bayes Theorem
Recall Bayes Theorem, which provides a way of calculating the posterior probability:
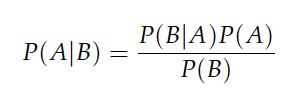
Before we go into more specifics of the Naive Bayes Algorithm, we'll go through an example of classification to determine whether a sports team will play or not based on the weather.
To start, we'll load in the data, which you can find here.
import pandas as pd
f1 = pd.read_csv("./data/weather.csv")
Before we go any further, let's take a look at the dataset we're working with. It consists of 2 columns (excluding the indices), weather and play. The weather column consists of one of three possible weather categories: sunny, overcast, and rainy. The play column is a binary value of yes or no, and indicates whether or not the sports team played that day.
f1.head(3)
Weather Play
0 Sunny No
1 Overcast Yes
2 Rainy Yes
Frequency Table
If you recall from probability theory, frequencies are an important part of eventually calculating the probability of a given class. In this section of the tutorial, we'll first convert the dataset into different frequency tables, using the groupby() function. First, we retrieve the frequences of each combination of weather and play columns:
df = f1.groupby(['Weather','Play']).size()
print(df)
Weather Play
Overcast Yes 4
Rainy No 3
Yes 2
Sunny No 2
Yes 3
dtype: int64
It will also come in handy to split the frequencies by weather and yes/no. Let's start with the three weather frequencies:
df2 = f1.groupby('Weather').count()
print(df2)
Play
Weather
Overcast 4
Rainy 5
Sunny 5
And now for the frequencies of yes and no:
df1 = f1.groupby('Play').count()
print(df1)
Weather
Play
No 5
Yes 9
Likelihood Table
The frequencies of each class are important in calculating the likelihood, or the probably that a certain class will occur. Using the frequency tables we just created, we'll find the likelihoods of each weather condition and yes/no. We'll accomplish this by adding a new column that takes the frequency column and divides it by the total data occurances:
df1['Likelihood'] = df1['Weather']/len(f1)
df2['Likelihood'] = df2['Play']/len(f1)
print(df1)
print(df2)
Weather Likelihood
Play
No 5 0.357143
Yes 9 0.642857
Play Likelihood
Weather
Overcast 4 0.285714
Rainy 5 0.357143
Sunny 5 0.357143
Now, we're able to use the Naive Bayesian equation to calculate the posterior probability for each class. The highest posterior probability is the outcome of prediction.
Calculation
Now, let's get back to our question: Will the team play if the weather is sunny?
From this question, we can construct Bayes Theorem. Because the know factor is that it is sunny, the P(A | B) becomes P(Yes | Sunny). From there, it's just a matter of plugging in probabilities.

Since we already created some likelihood tables, we can just index P(Sunny) and P(Yes) off the tables:
ps = df2['Likelihood']['Sunny']
py = df1['Likelihood']['Yes']
That leaves us with P(Sunny | Yes). This is the probability that the weather is sunny given that the players played that day. In df, we see that the total number of yes days under sunny is 3. We take this number and divide it by the total number of yes days, which we can get from df:
psy = df['Sunny']['Yes']/df1['Weather']['Yes']
And finally, we can just plug these variables into bayes theorem:
p = (psy*py)/ps
print(p)
0.6
This tells us that there's a 60% likelihood of the team playing if it's sunny. Because this is a binary classification of yes or no, a value greater than 50% indicates a team will play.
Source: https://www.analyticsvidhya.com/blog/2015/09/naive-bayes-explained/
Not indicating that the content you copy/paste is not your original work could be seen as plagiarism.
Some tips to share content and add value:
Repeated plagiarized posts are considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
Creative Commons: If you are posting content under a Creative Commons license, please attribute and link according to the specific license. If you are posting content under CC0 or Public Domain please consider noting that at the end of your post.
If you are actually the original author, please do reply to let us know!
Thank You!
Congratulations @lesley2958! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @lesley2958! You have received a personal award!
Click on the badge to view your Board of Honor.
Congratulations @lesley2958! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!