The easiest way to understand Elliptic Curve (EC), point addition, scalar multiplication and trapdoor function; explained with simple graphs and animations.
1. Abstract
What the heck is an elliptic curve?
A plane algebraic curve defined by an equation of this form: y2 = x3 + a*x + b
Why are elliptic curves important in cryptography?
Because elliptic curve scalar multiplication is a trapdoor function
How does scalar multiplication works?
Scalar/point multiplication is defined as repeated addition of a point to itself
How does point addition works then?
If we draw a line passing thru elliptic curve points (or draw a tangent to a single point) it will intersect another point on the curve and the inverse of this intersection point is the result of point addition
Since a picture is worth a thousand words then the following elliptic curve point addition/multiplication animation has 33 frames and is worth a lot more, do the math.
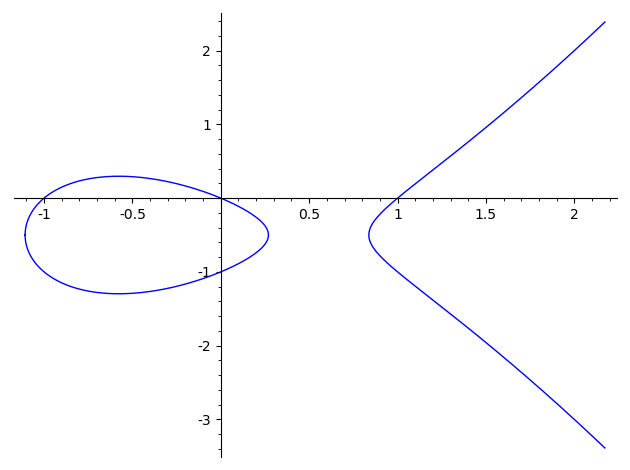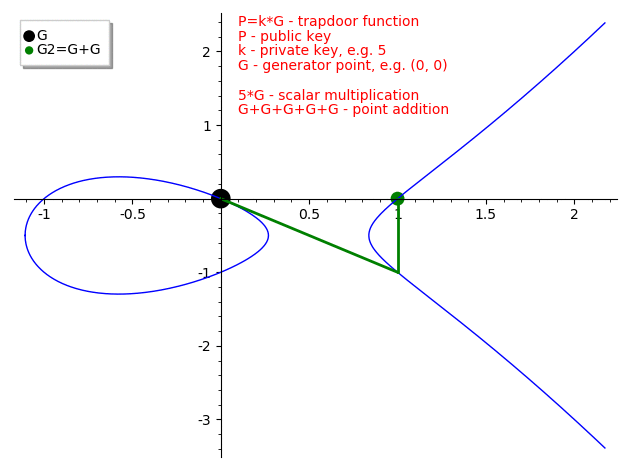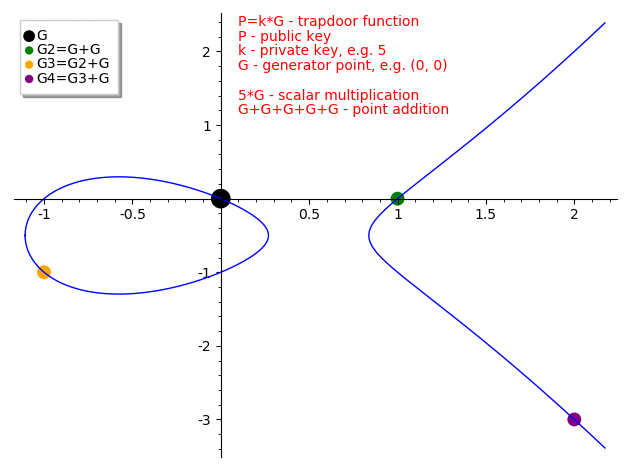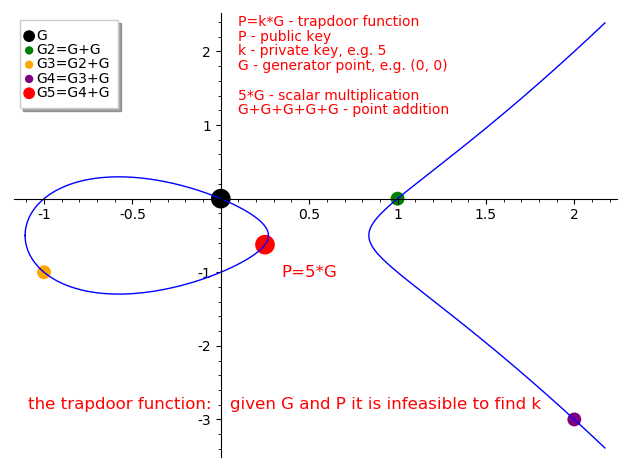
Given an elliptic curve E a point on elliptic curve G (called the generator) and a private key k we can calculate the public key P where P = k * G.
The whole idea behind elliptic curves cryptography is that point addition (multiplication) is a trapdoor function which means that given G and P points it is infeasible to find the private key k.
Read the blog post for more details.
Nice article, very clear