Coursera에 올라온 Bitcoin and Cryptocurrency Technologies 강의를 들으며 정리한 내용입니다.

첫 번째 글의 주제는 해시 함수입니다. 암호화폐에서 해시 함수는 매우 중요한 역할을 합니다. 인증부터 마이닝까지 암호화폐의 바탕을 이루는 기술들엔 모두 해시 함수가 적용되어 있습니다. 따라서 암호 화폐 이해를 위해선 해시 함수에 대해 꼭 이해하고 넘어가야 합니다.

그럼 해시 함수에 대해 간략히 소개한 후 해시 함수가 갖는 세 가지 장점인 Collision-free, Hiding, Puzzle-friendly가 암호 화폐에서 어떤 역할을 하는지 알아보겠습니다.

Hash Function

해시 함수는 임의의 길이를 갖는 데이터를 고정된 길이의 데이터로 사상하는 함수입니다.

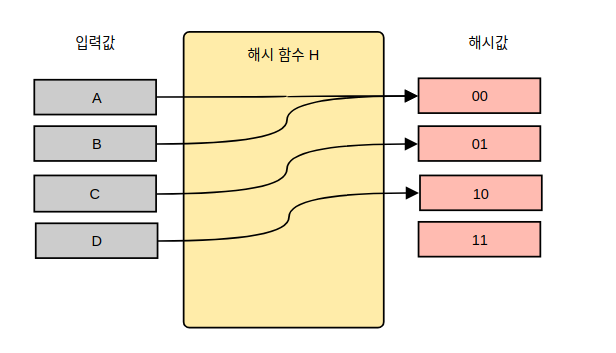
위의 그림은 A, B, C, D라는 네 가지 입력값에 대해 해시 함수 H를 적용한 모습입니다.

해시 함수 H는 2bit의 고정된 길이를 가지는 함수입니다. 1bit는 0과 1을 가질 수 있습니다. 따라서 2bit 길이의 해시값은 2^2 = 4가지 경우의 수를 가집니다.

A의 해시값은 00, B의 해시값은 00, C의 해시값은 01, D의 해시값은 10입니다.

A와 B의 경우 00이라는 같은 해시값을 가집니다. 앞서 해시 함수가 임의의 길이를 갖는 데이터를 입력으로 받는다고 했는데요. 입력의 경우의 수가 무한하다는 말입니다. 반면 해시값은 고정된 길이로 유한한 값을 가집니다. 따라서 A, B와 같이 다른 입력이 같은 해시값을 가지는 경우는 반드시 나옵니다. 이를 해시 충돌이라고 합니다. 해시 충돌에 대해선 아래에서 다시 한번 설명하겠습니다.

해시 함수는 암호학과 컴퓨터 공학 등 매우 많은 분야에서 사용되며 그 종류 또한 다양합니다. 크게 암호학적 해시 함수와 비암호학적 해시 함수로 구분합니다. 해시값으로부터 입력값의 관계를 찾기 어려운 성질을 가지는 경우 암호학적 해시 함수라고 부릅니다.

앞서 암호 화폐에서 해시 함수가 많이 쓰이고 있다고 말했습니다. 암호 화폐는 암호학적 해시 함수를 사용합니다.그중 암호화폐의 대장 격인 비트코인에서 쓰이는 해시 함수가 바로 SHA256 함수입니다.

SHA256은 미국 국가안보국(NSA)에서 설계하고 미국 표준으로 지정된 해시 함수입니다. 그만큼 안전하게 오랜 기간 검증된 함수입니다. 아직 공격 성공 사례 또한 발견되지 않았습니다.

여기서 공격 성공 사례라는 말이 아리송한 분이 있을겁니다. 해시 함수는 수학 공식일뿐인데 공격이라는건 무슨 말일까요?

앞서 암호학적 해시 함수가 해시값으로부터 입력값의 관계를 찾기 어려운 성질을 만족하는 경우라 말했습니다. 따라서 해시 함수에 대한 공격이란 해시값과 입력값의 관계를 파악하는 것을 말합니다. 예를 들어 해시 충돌 사례가 발견되었다면 그 함수는 안전하지 않은 함수라고 말할 수 있습니다.

SHA256 함수는 아직까지 충돌 사례를 단 한 번도 발견하지 못했습니다.

해시값의 길이는 유한하기 때문에 충돌은 무조건 발생할 수밖에 없다고 했습니다. 그런데 충돌 사례를 발견하지 못했다니, 이해가 안갈 수 있습니다. 그건 sha256 함수의 해시값 경우의 수가 매우 크기 때문입니다. 이건 아래에서 실습을 해보며 직접 체험해보겠습니다.

아래 사이트에서 해시 함수를 실험해 볼 수 있습니다.

http://www.md5calc.com/sha256

저는 암호화폐 어려워라는 데이터에 해시 함수를 적용했습니다. 그럼 해시값은,

04f2d79320c92311ba910d66b589ab88efe30204c9914c9b1cb5554e21958b18

이 나옵니다. 같은 문자를 적용해보시면 같은 해시값이 나오는 걸 보실 수 있습니다.

위 문자를 다시 한번 보시죠. 길이를 세어보면 총 64자입니다. 정확하겐 0~9와 a~f의 한 자리당 16개의 수가 나올 수 있는 16진수입니다. 16진수 64자리. 256bit입니다. 256bit의 해시값의 경우의 수는 2^256 개입니다. 얼마나 큰 수 일까요? 얼핏 보면 그리 크지 않아 보이기도 하고, 감이 잘 오지 않습니다.

그럼 이를 10진수로 표현하면,

115792089237316195423570985008687907853269984665640564039457584007913129639936

자릿수는 78자리입니다.

현실 세계 사례와 비교하면 조금 더 감이 옵니다. 사실 이 정도 수는 비교할만한 대상을 찾기도 어려운 매우 큰 수입니다. 이와 비슷한 수를 찾자면 (현재 알려진) 우주의 원자 개수가 있습니다. 대략 10^80개입니다.

수가 큰 게 무슨 의미인가 싶겠지만, 이는 해시 함수의 안정성이 높음을 뜻합니다.

앞서 해시 충돌 사례가 발견되면 안전하지 않은 함수라고 말했습니다. 그럼 해시 충돌을 발견하려면 어떻게 해야 할까요? 해시값이 입력값에 대해 고르게 분포한다면 방법은 한 가지밖에 없습니다. 최대한 많은 경우의 수를 테스트해보는 겁니다.

이를 무차별 대입 공격(Brute-Force Attack)이라고 합니다. 될 때까지 무식하게 해보는 것이죠.

256bit 해시 함수의 경우 대략 2^130개 정도의 입력을 테스트하면 충돌 사례를 발견할 확률이 대략 99.8%라고 합니다.

현재 비트코인의 초당 해시 함수 계산량(hash rate)은 2018년 3월 8일 기준으로 26499460 TH/s 입니다. 1 TH는 초당 1,000,000,000,000 의 해시를 계산함을 말합니다.

그럼 2^130개의 해시값을 계산하려면?

5.136 * 10^19초이며, 1.628 * 10^12년이 걸립니다. 이는 우주 나이의 120배이고, 태양 나이의 360배입니다.

해시 충돌 사례를 찾으려면 비트 코인 채굴에 참여하는 모든 컴퓨터를 동원해도 이만큼 오랜 시간이 걸립니다. 그만큼 해시 충돌 사례를 찾는 건 어렵습니다.

물론 한 가지 가정이 필요합니다. 앞서 언급한 입력값에 대해 고르게 분포해야 한다는 것입니다. 예를 들어 특정 데이터를 조금 바꾼 해시값을 계산하니 해시값 차이가 크게 안난다면? 값을 조금씩 바꿔보면 해시 충돌 찾는 게 쉬워지겠죠. 따라서 데이터가 조금이라도 달라진다면 해시값이 크게 달라져야 합니다. 이를 쇄도 효과라고도 합니다.

SHA256 함수는 현재까지 이 조건을 잘 만족하는 것으로 보입니다. 따라서 안전한 해시 함수로 여겨지죠. 나카모토 사토시가 비트코인에 SHA256 함수를 채택한 이유입니다.

하지만 (SHA256 해시 충돌 가능성에 대한) 예외가 하나 있습니다. 바로 양자 컴퓨팅입니다. (이론적으로) 양자 컴퓨팅을 사용하면 계산 성능을 획기적으로 늘리는 게 가능합니다.

양자 컴퓨터가 본격적으로 사용된다면 SHA256 해시 함수를 쓰는 비트코인이 위협을 받을거란 의견도 있습니다. 물론 답변에서 보듯이 양자 컴퓨팅이 정말 한순간에 보편화하지 않는 이상 그럴 가능성은 적으니 걱정하지 않아도 됩니다.

지금까지 알아본 해시 함수에 대해 정리하면,

해시 함수는 특정 입력을 고정 길이를 가진 임의의 해시값으로 바꿔주는 함수입니다.
무한한 입력 대비 고정된 출력을 합니다. 따라서 해시 충돌이 발생 가능성이 항상 존재합니다.
비트코인은 SHA256 해시 함수를 사용합니다.
SHA256 함수의 해시값은 256bit 길이를 가지므로 해시 충돌 가능성이 매우 낮습니다. 이러한 안정성 때문에 비트코인은 SHA256 함수를 사용합니다.

이러한 해시 함수는 기밀 유지, 데이터의 무결성 보증, 인증, 부인 방지 등 암호학의 여러 분야에서 사용되고 있습니다. 암호 화폐에서도 이러한 기술을 모두 쓰고 있죠.

그럼 지금부터 해시 함수의 성질을 활용해 어떤 일을 할 수 있는지, 그리고 그 성질을 암호화폐에서 어떻게 사용하고 있는지 알아보겠습니다. 아직 어리둥절하신 분이 많겠지만 아래 설명을 본다면 해시 함수가 암호 화페에서 어떻게 사용되는지 조금은 감을 잡으실 수 있을 겁니다. 암호화폐는 비트코인을 기준으로 설명하겠습니다.

Hash Function Properties

SHA256 함수와 같은 암호학적 해시 함수는 아래 세 가지 유용한 성질을 가집니다.

collision-free : 해시 함수를 적용한 임의의 두 결과값이 같은 해시값을 같을 확률이 무시할 정도로 낮다.
hiding : 해시 함수의 결과값에서 입력값을 추정하기 어렵다.
puzzle-friendly : 해시값이 고정된 길이를 갖고 랜덤하게 해시값이 분포되는 점을 활용해 손쉽게 계산 문제를 만들 수 있다.

위 세 성질과 암호화폐에서의 쓰임새에 대해 알아보겠습니다.

Collision-free

첫 번째 성질은 Collision-free 입니다. 이는 해시 충돌이 발생할 확률이 무시 가능할 정도로 낮다는 것을 말합니다. 먼저 해시 함수 개념에 관해 설명할 때 SHA256 함수의 해시 충돌 가능성 얘기가 기억나실 겁니다.

충돌 가능성이 적다면, A라는 임의의 데이터가 유일한 해시값을 가진다고 가정할 수 있습니다.

사람의 지문을 생각하면 됩니다. 신분증 만들 때 지문 등록하시는 것 기억하시나요? 어떤 사람인지 알아보기 위해 모든 데이터가 필요하지 않습니다. 지문이 같은 확률이 매우 적다는 가정하에 지문만 저장해서 사람을 인식하는데 사용할 수 있습니다.

해시 함수도 마찬가지입니다. 데이터가 어떤 데이터인지 알기 위해 모든 데이터를 활용하지 않고 해시 함수를 통해 나온 해시값으로 판단할 수 있습니다. 데이터 지문이라고 보시면 됩니다.

이미 일상생활의 많은 곳에서 이 성질을 활용하고 있습니다. 지문 사례와 같이 데이터가 전과 같은 데이터인지 확인하기 위해 전과 같은 정보를 그대로 저장하는 대신 256bit의 짧은 데이터만 사용해 저장하고 같은지 확인하는 것이죠. 또한, 데이터가 조금이라도 달라져도 해시 함수값도 달라지기 때문에 데이터 전송 도중 도중 손실이나 악의적인 변조가 있었는지 확인하기 위해서도 사용할 수 있습니다.

그럼 암호화폐에서 사용 사례는 어떨까요? 관심 있으신 분이라면 암호화폐에 한 번 기록된 정보는 조작할 수 없다는 얘기를 들어보셨을 겁니다. 데이터에 불과한 거래 장부를 어떻게 조작하지 못하게 막을 수 있을까요? 여기서 해시 함수가 사용됩니다.

비트코인의 블록을 한 번 봅시다.

비트코인은 블록은 10분에 한 번씩 생성됩니다. 한 블록엔 여러 가지 거래 기록(Transactions)이 담겨져 있죠. 비트코인은 이러한 블록을 연결한 겁니다. 그래서 말 그대로 블록체인이라고 불리는 겁니다.

블록체인을 그림으로 간단하게 그려보면 아래와 같습니다.

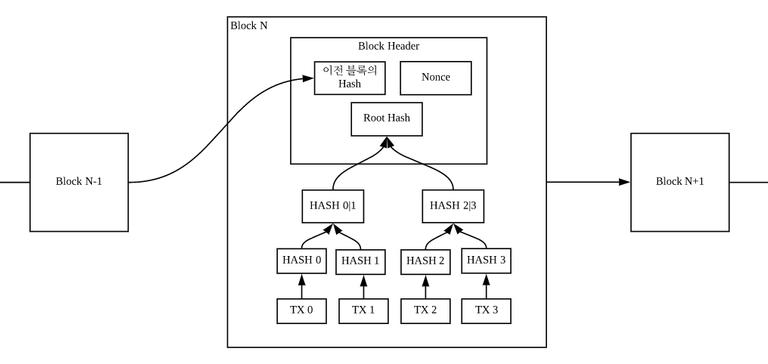
N 번째 블록을 봅시다. 4개의 거래 기록(TX0, TX1, TX2, TX3)이 담긴 블록입니다. 각각의 거래 데이터는 해시값으로 변경되어 모든 거래가 합쳐진 하나의 해시값인 루트 해시값이 됩니다. 그리고 블록 헤더는 이전 블록의 해시, 루트 해시, Nonce(마이닝에서 사용되는 값입니다)로 구성됩니다. 이 세 값이 합쳐져 다시 해시값을 계산하고 이게 블록의 해시값이 됩니다.

그럼 만약 A라는 공격자가 블록 트랜잭션 중 하나를 악의적으로 변경하려고 한다면 어떻게 될까요? 예를 들어 100 BTC를 자신의 지갑으로 보내도록 트랜잭션 정보를 조작하는 겁니다. TX0 거래 기록에 조작을 시도합니다. 그럼 TX0의 해시값인 HASH 0의 값이 완전히 변경됩니다. Collision-free 특성에 따라 임의의 데이터의 해시값은 유일하다고 가정할 수 있기 때문이죠. 연쇄적으로 HASH 0 값을 포함한 해시값들인 HASH 0|1, Root Hash, Block Hash까지 모두 변경이 됩니다.

그럼 A 공격자가 조작한 정보를 받아들여달라고 비트코인 피어(참여자들)에게 전달합니다. 정보를 받은 피어들은 장부가 조작되지 않았는지 확인합니다. 어떻게 확인할까요? 자신들의 노드에 기록된 거래정보에 따라 해시값을 계산해보고 A가 제안한 블록과 해시값을 비교하는 겁니다. 해시값이 다르다면 어딘가 데이터가 1이라도 조작된 것이 분명합니다. 따라서 피어들은 이 블록을 기각하고 유효하지 않다고 생각합니다. 해당 블록에 더 체인을 쌓지 않게 됩니다. 아무도 인정하지 않는 블록이 되는 것이죠. 따라서 공격은 실패하게 됩니다.

블록의 해시값을 계산할 때 이전 해시값을 쓰기 때문에 과거 장부를 조작하는 것도 불가능합니다. 예전 블록의 데이터를 조금이라도 조작하면 해시값이 크게 달라지기 때문입니다.

Hiding

Hiding은 high-min entropy 분포를 가지는 임의의 값 r과 데이터 x, 이 둘을 더해 해시 함수를 적용한 H(r|x) = y의 값이 있을 때 해시값(y)로 x 값을 알아내는 것이 매우 어려움을 말합니다. x라는 데이터를 임의의 값 r과 결합해 숨긴채로 상대방에게 전달하는 겁니다.

어떻게 이용되는지 쉽게 이해가 가는 개념은 아닙니다. 조금 더 자세히 살펴보도록 합시다.

해시 함수 개념에 관해 얘기할 때 충돌을 발견하려면 무작위 공격밖에 방법이 없다는 것과 같은 논리입니다. 어떤 값을 넣어야 H(x)가 나오는지는 여러 값을 해시 함수에 넣어보는 수밖에 없습니다.

물론 모든 사례에 적용되는 건 아닙니다. 입력의 경우의 수가 많지 않고 공격자가 이를 알 수 있다면 쉽게 추론할 수 있죠.

동전 던지기를 생각해봅시다.

Alice와 Bob이 동전 던지기 게임을 합니다. Alice가 동전을 던지고 그 결과를 Bob에게 전송하고, Bob은 Alice가 어떤 동전을 던졌는지 맞추는 게임입니다. Bob이 결과를 맞추면 Bob이 이깁니다. 문제는 Alice는 한국에, Bob은 미국에 있다는 겁니다.

게임을 시작합니다. Alice가 Bob에게 '앞'이라고 말합니다. Bob은 동전 던지기를 합니다. '앞'이 나오지만 게임에서 이기기 위해 Alice에게 '뒤'가 나왔다고 합니다. 이런 상황에선 서로를 믿을 수 없어 게임 진행이 되지 않습니다.

Alice는 데이터를 숨기기 위해 앞/뒤 값을 해싱해서 보냅니다. Bob은 해시 된 값만 보기 때문에 처음 몇 번은 어느 쪽인지 알지 못합니다. 하지만 결과를 보고 나서 해당 값이 동전의 앞 뒤 중 어디를 뜻하는지 알게 됩니다.

x는 동전을 던졌을 때 나올 수 있는 경우의 수라면, x = {앞, 뒤}가 가능합니다. 해시값은 H('head')와 H('tail') 이 됩니다. 이 해시값의 입력 x는 찾기 쉽습니다. 앞과 뒤의 해시값을 계산하고 값을 비교하면 됩니다.

따라서 해시값을 쓰는 것도 통하지 않습니다. 그럼 어떻게 해야 할까요? 문제는 x의 입력으로 오직 두 가지 경우의 수가 있다는 것입니다.

이를 피하고자 임의의 값 r을 하나 뽑아 x값과 결합해 이 값을 해시 함수(H(r|x))로 적용해봅시다. 그럼 r 값에 따라서 해시값이 매우 달라집니다.

주의할 점은 임의값 r의 분포는 high min-entorpy를 가져야 한다는 겁니다.

high min-entropy 는 값이 일정하게 분포되어 있음을 말합니다. 데이터의 분포가 특정 패턴을 따른다면 탐색 공간이 더 좁아지기 때문에 해시 함수의 패턴을 파악하기가 쉬워집니다. 따라서 최대한 high min-entorpy 분포에 가까운 키 값을 선택해야 합니다.

다시 정리하면, Hiding이란 high min-entropy를 가지는 분포에서 임의의 수 r을 뽑아 H(r|x)를 x의 해시 함수로 쓴다면 그 해시값으로부터 x의 값을 추정하기 매우 어렵다는 말입니다. 데이터를 숨겨서 보낼 수 있죠. 물론 해시값의 입력을 추정하고자 하는 상대가 r의 값을 몰라야 합니다.

그럼 Hiding을 이해한 Alice가 새로운 게임 방식을 제안합니다. 동전의 앞/뒤 예측값 x와 임의의 비밀키 r을 조합한 해시값을 bob에게 보냅니다. bob은 해시값으로부터 동전의 앞/뒤를 알 수가 없습니다. bob이 동전을 던져 나온 결과를 Alice에게 보냅니다. 그럼 Alice는 비밀키 r과 예측값 x를 보냅니다. Bob은 이 두 값을 조합해 해시 함수를 적용한 후 여기서 나온 해시값이 Alice가 처음에 보낸 해시값과 맞는지 확인합니다.

이 방식이라면 아무리 멀리 떨어져 있어도 조작할 수 없습니다. Alice가 비밀키를 보내주기 전에는 Bob이 해시값에서 동전 앞/뒤를 알 수가 없기 때문이죠. 마찬가지로 Alice도 게임 결과에 영향을 미치지 못합니다. 자신이 x라는 값을 골라 보냈다는 걸 숨길 수 없기 때문입니다.

게임을 다시 할 때는 Alice가 새로운 비밀키를 선정해 게임을 하면 됩니다. 서로 믿고 게임을 진행할 수 있습니다.

이처럼 메시지를 숨긴 채 상대방에게 보내고 후에 메시지를 열어볼 수 있는 키를 보내 확인하는 방식을 Commitment scheme이라고 합니다.

매우 단순화한 프로토콜이지만 이러한 방식을 응용해서 신원확인이나 부인방지, 인증 등에 사용하고 있습니다.

당연히 암호화폐에서 쓰이고 있습니다. 물론 위에 단순화한 사례보다는 훨씬 복잡한 방식이긴 하지만 원리 자체는 같다고 보시면 됩니다. 비트코인 지갑의 개인키/공개키부터 누군가에게 비트코인을 전송할 때 서명을 하는 것까지 매우 다양한 영역에서 사용되고 있습니다.

Puzzle-Friendly

어떤 해시 함수 H와 high min-entorpy 분포를 가지는 임의의 값 k와 데이터 x, 이 둘을 결합한 해시값 z(H(k|x))가 있습니다. 이 때 k와 z가 주어진 경우 x 값을 찾기가 매우 어렵다는 걸 Puzzle-Friendly하다고 합니다. 위의 Hiding 과 유사해보입니다. k 값을 주느냐 아니냐 차이가 있죠.

정의만 보면 이해하기 쉽지 않습니다. 아래 예시를 보면 이 성질의 유용함을 알 수 있습니다.

여러분이 어떤 퍼즐 문제를 하나 내려고 합니다. Puzzle-Friendly 정의와 같이 k와 해시값인 y가 주어졌을 때 x를 찾는 문제입니다.

k는 퍼즐 id로 입니다. high-min entropy를 가지는 분포에서 뽑힌 임의의 값입니다.
8bit 의 해시값을 가지는 해시 함수 H를 사용합니다. 나올 수 있는 경우의 수는 2^8 = 256입니다. 0~255 사이의 값을 가집니다.

그럼 이렇게 계산 문제를 낼 수 있습니다.

해시값 H(k|x)가 y값보다 작은 x값을 찾아라.

y = 2^6이라고 합시다. 해시 함수 H는 0 ~ 255 사이의 값을 가질 수 있다고 했습니다. 그럼 임의의 값 x가 위 조건을 만족할 확률은 2^6 / 2^8 = 1 / 2^2 = 1 / 4 = 0.25, 25%가 됩니다.

첫 번째 문제를 진행한 뒤에 같은 문제를 내려면 퍼즐 id인 k 값만 바꿔서 진행하면 됩니다. 해시 함수는 쇄도 효과에 의해 일부분만 바뀌어도 해시값 자체가 크게 달라지니 이전 문제의 결과에서 다음 문제 패턴을 알 수 없습니다. 완전 새로운 문제가 되는 것이죠.

근데 문제가 너무 쉽습니다. 그럼 y 값을 바꾸면 됩니다. y를 2^6이 아니라 2^4로 조정해봅시다. 그럼 확률은 2^4 / 2^8 = 0.0625, 6.25%가 됩니다.

위와 같은 방식으로 임의의 계산 문제를 무한히 만들어 낼 수 있습니다.

암호화폐에서도 Puzzle-Friendly 성질을 활용한 계산 문제를 사용하고 있습니다. 암호화폐의 채굴에 대해 들어보신 분이라면 채굴이 문제를 풀고 그걸 가장 빨리 푼 사람에게 보상을 주는 것이라는 말을 들어보셨을 겁니다. 여기서 나오는 문제가 위의 해시값을 찾는 계산 문제입니다.

비트코인 블락을 다시 한 번 봅시다.

비트코인은 계산 문제를 푸는 사람이 트랜잭션이 담긴 블록을 블록 체인 위에 추가하게 됩니다.
계산 문제는,

해시값 H(k|x)이 y값보다 작은 x값을 찾아라.

라고 했는데요.

여기서 k는 이전 블록의 해시값과 루트 해시값이 됩니다. 그리고 x는 Nonce가 됩니다. y를 target이라고 합니다. target 값이 문제의 난이도를 조절하는 제약조건이 됩니다. target은 비트코인 마이닝에 참여하는 모든 노드가 공유합니다.

Nonce 값을 증가시키면서 target 값보다 작은 값을 찾는 겁니다. target이 작을수록 난이도는 더 올라갑니다.

이러한 방식으로 비트코인 마이닝이 이루어집니다. 참여하는 사람들이 많아져 계산량이 늘어난다면 인플레이션이 발생하니 Target 값을 줄여가며 난이도를 조정합니다.

마이닝이 완료되어 블록을 전파하면 사람들은 해당 마이닝이 올바르게 이루어졌는지 Nonce 값(x)과 해시값(k)을 해싱해서 Target 보다 작은지 확인합니다. 데이터를 통해서 해시값을 만드는 것은 금방 할 수 있기 때문에 해답을 검증하는 것은 쉽고 빠르게 할 수 있습니다. 검증이 완료되면 올바른 블록이라 판단하고 체인 위에 블록을 올립니다.

이러한 과정을 작업 증명(PoW)라고도 합니다.

2018년 3월 11일에 마이닝 된 513022번 블록을 봅시다.

해시값이 0으로 시작하는 걸 볼 수 있습니다. 이 0이 많을수록 난이도가 높아집니다. Target 수보다 적어야 하니 앞자리는 0이 올 수밖에 없죠. 해시 난수(Nonce)가 x값이 됩니다. 해당 Nonce 값과 트랜잭션의 해시값들, 이전 해시값을 조합해 현재 블록의 해시값(Target보다 작은)이 만들어집니다.

마이닝의 난이도는 2주에 한 번씩 조정됩니다. 즉 Target이 2주에 한 번씩 바뀌는 겁니다. 난이도는 10분에 한 블록을 마이닝 할 수 있을 정도, 즉 10분에 한 문제를 풀 수 있는 수준으로 조정됩니다. 현재 비트코인 마이닝에 참여하는 사람들이 늘고 있으니 인플레이션을 막기 위해 난이도는 점점 더 높아집니다.

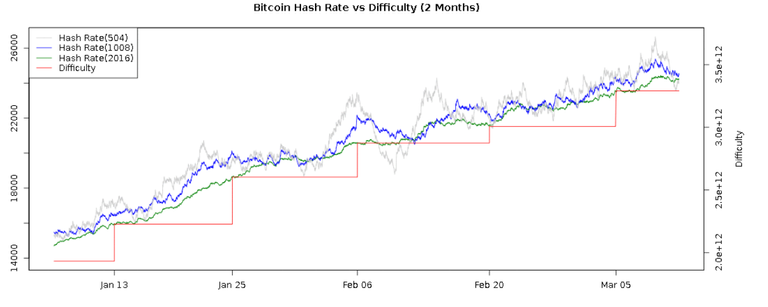
위 차트를 통해 2주에 한 번씩 마이닝 난이도가 높아지는 모습을 확인할 수 있습니다.

마치며

해시 함수는 임의의 데이터를 고정 길이의 데이터로 변환하는 함수로, 해시값에서 입력값을 추론하기 어려운 성질을 갖고 있습니다. 본 글에서는 해시 함수의 개념과 Collision-free, Hiding, Puzzle-Friendly 성질과 암호화폐에서의 쓰임세에 대해 간략히 알아보았습니다.

다음 글에서는 이중 지불 문제와 블록 체인의 개념, 그리고 지금까지 배운 내용을 통해 간단한 암호화폐를 만드는 방법에 대해 설명하겠습니다.