Hi everyone!

Today I'll talk a little about RaiBlocks and its application. RaiBlocks is a DAG-based ledger that allows for ZERO-FEE transactions that are almost instant! Unlike Bitcoin, which can take days to process and has extremely high transaction fees (upwards of 20% for some transactions!) XRB is built on a completely different, but related, technology known as a Direct Acrylic Graphic.

DAG works differently than the blockchain. Where the blockchain requires Proof of Work from miners on each transaction the DAG gets around this by getting rid of the block entirely. Instead, DAG transactions are linked from one to another, meaning one transaction confirms the next and so on. These links are where the term DAG comes from, just like blocks getting hashed are where the blockchain receives its name.

Because of this revolutionary technology, RaiBlocks is able to complete transactions almost instantly, and with zero transaction fees!

On top of that, RaiBlocks has the ability to scale massively as its network grows, by supporting upwards of 7,000 TPS (transactions per second). Here is a graphic comparing this amazing statistic to other popular cryptos.

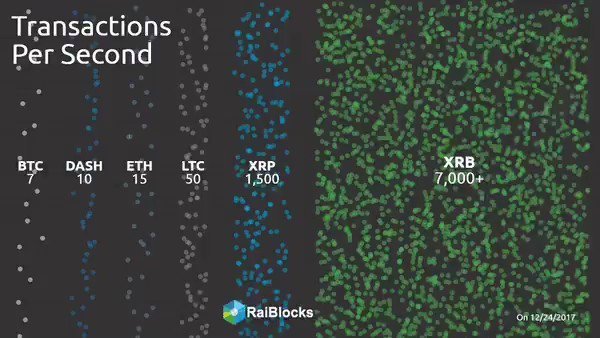
If I haven't convinced you yet...

RaiBlocks also has a low circulating supply (<130,000,000) and is not even listed on any major exchanges yet!
Most important of all, they won the December Binance coin of the month vote, so once they are listed there I believe it is going to absolutely explode. The technology is definitely there, the support is there, the scalability is there, the development and marketing team are there, all it needs now is the spark. Sign up on Binance now so you can be ready for when XRB drops!

Sign up Here!!:
http://bit.ly/2mi5qaH

Disclaimer: I am invested in XRB myself, simply because I fully believe in it and see it as the future of digital currency!

Thanks for reading! Upvote, comment, and Resteem to show everyone the power of RAIBLOCKS.