포트폴리오의 필요성
투자론이 다루는 포트폴리오 이론들은 박사과정을 거친 퀀트들이 짜내는 것들에 비하면 매우 기초적인 수준의 회귀분석, 통계 지식, 금융에 대한 이해를 요구합니다. 하지만 절대 다수의 투자자들은 나의 상품들을 한 바구니에 담는 것과 같은 어떤 체계적인 포트폴리오의 필요성을 크게 느끼지 못하는 듯 합니다. 봉과 이동평균선, 차트를 읽는 데에 올인하거나 상품의 자의적인 가치평가를 기반으로 '재료'니 '호재'니 하는 것들에 내 모든 자산을 들었다 놨다 하는 분들을 많이 만났습니다. 그러나 이는 어떤 종목들을 선정할 것인가, 투자의 가부 결정을 내리는 분석 단계만 밟고 금융시장에 뛰어드는 꼴입니다. 안정적인 포트폴리오는 나의 금융자산이, 나아가 내 삶이 몇 번의 풍파에도 쉽게 흔들리지 않게끔 하는 단단한 키와 길잡이입니다. 이미 일확천금, 마진거래 외에는 거들떠도 보지 않는 분들에게는 이번 글 또한 별 의미가 없을 것임을 알고 있지만, 누구나 할 수 있고 실제로도 효과를 많이 보고 있는 이론이기에 시간을 할애해 설명해보고자 합니다.
이론적 배경

본 이론을 만들어 낸 클로드 섀넌은 수학과 전기공학을 연구하며 정보 이론, 디지털 회로 이론의 선구자라 불리는 학자입니다. 전공과 별로 연관 없는 금융에서 그의 이론은 자산의 수익률이 극대화되기 위해서는 기하평균이 높아야 한다는 기본적인 수학 원리에서부터 출발합니다.
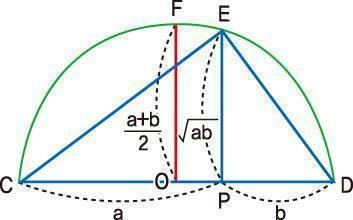
흔히들 사용하는 산술평균은 (a+b)/2와 같이 단순히 수익률의 평균이라면, 기하평균은 각 수익률을 곱한 뒤, 이에 대해 제곱근을 취하여 계산하게 됩니다. 투자의 성패는 원금 대비 몇% 증가했는가를 보고 따지게 되므로, 일반적으로 기하평균을 통해 수익률을 산출하고 있습니다.
평균수익률의 함정, 고수익 고위험 상품의 문제를 이를 통해 이해할 수 있습니다. 예를 들어 기대수익률 5%의 상품1과 10%의 상품2가 존재하여 1달러씩 투자했다고 생각해봅시다. Risk와 횡보에 의해 수익과 손실이 번갈아가며 나타나며, 손실은 기대수익률과 같은 수준이라 가정합니다.
1일차
상품 1 : 1 * 1.05 = 1.05달러
상품 2 : 1 * 1.1 = 1.1달러
2일차
상품 1 : 1 * 1.05 * 0.95 = 0.9975달러
상품 2 : 1 * 1.1 * 0.9 = 0.99달러
20일차
상품 1 : 0.975279 달러 (기하평균 : 하루평균 약 0.125% 수익)
상품 2 : 0.904382 달러 (기하평균 : 하루평균 약 -0.5% 수익)
산술평균으로는 같은 기대값을 보이지만, 기하평균의 관점에서는 수익률이 2배 높은 상품의 손실액이 4배나 높다는 것을 알 수 있습니다. 간단히 말해 당장에 높은 수익률을 보이는 자산에 돈을 쏟는 것이, 장기적으로는 오히려 가장 큰 손해를 볼 선택이 될 가능성이 높다는 이야기입니다. 금융자산의 복리수익률 최대화 문제는 위와 같은 기하평균을 어떻게 극대화시키고 리스크를 최소화 할 방법을 찾는 데에 달려 있습니다.
Shannon's Demon
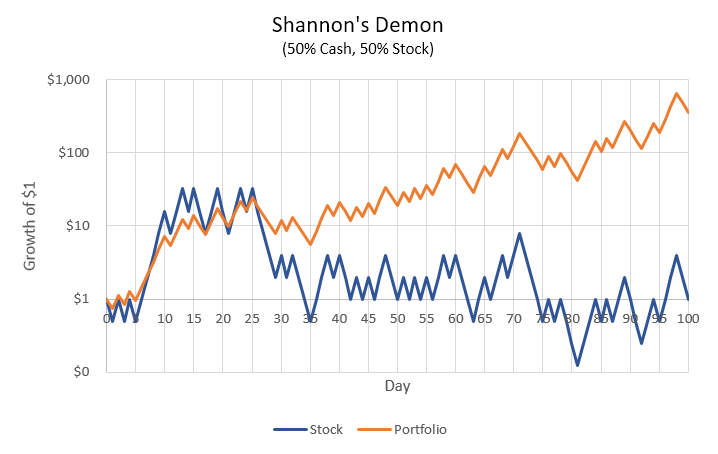
차트 : https://thepfengineer.com/2016/04/25/rebalancing-with-shannons-demon/
섀넌의 균형복원 포트폴리오는 기하평균을 극대화시키기 위해 현금과 위험자산의 비중을 각각 50% 씩 두어야 한다는 명제에서부터 출발했습니다. 상품과 현금의 비중이 각각 50 : 50 이어야 한다는 것을 대전제로 두고, 수익을 보면 그 수익의 절반을 현금화 하며, 손해를 보면 그 손해의 절반분을 다시 현금으로 메꿔 균형을 유지합니다. 이를 통해 수익의 일정치가 현금화되어 기하평균을 깎아먹을 가능성을 낮추고 수익은 지속적으로 얻을 수 있게 됩니다.
섀넌은 본 모델이 어떤 상황에서든 돈을 잃지 않을 수 있는 리밸런싱이지만, 현실적으로는 수수료와 세금 문제 때문에 어려울 것이라는 회의적인 입장이었습니다. 하지만 주식에서 수수료가 압도적으로 낮은 ETF나, 아직 법적으로 세금이 제도화되지 않고 특정 거래소에서 우대수수료로 거래할 수 있는 코인시장에서는 본 이론이 성공적인 결과를 보여줍니다. 위의 차트는 일일 수익률이 100% 혹은 -50%로 무작위로 섞이는 극단적인 모델이라 비현실적이지만, 위와 같은 지옥(?)에서도 본 모델이 성공적으로 생존할 수 있는 방안임을 보여주고 있습니다.
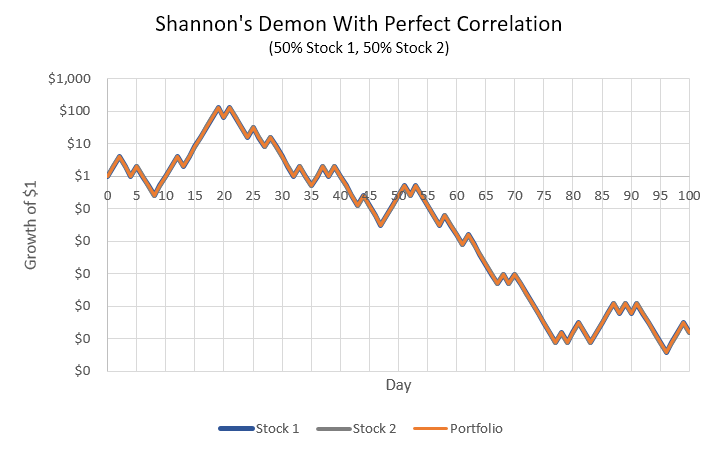
다만, 포트폴리오를 구성하는 자산들이 높은 상관관계를 보이는 경우 본 모델은 큰 의미를 갖지 못합니다. 상관계수는 두 자산의 함께 움직이는 정도를 공분산/(자산1의 표준편차 * 자산2의 표준편차)로 나타낸 것으로, -1과 1 사이의 값을 가집니다. 위의 차트는 두 자산이 완벽한 상관관계를 가지며 상관계수가 1일 때를 가정한 차트로서, 포트폴리오가 기존 자산들과 같은 길을 걷게 됨을 보여줍니다.
코인투자에의 현실적인 적용
따라서 효과적으로 본 모델을 적용하기 위해서는 서로 상관관계가 높지 않은 자산들을 포트폴리오에 담고, 지속적으로 현금과 투자자산의 비율을 5:5로 유지하는 것이 핵심이라 할 수 있습니다. 저번 마코위츠 포트폴리오 글에서 말씀드린 부분을 오늘도 반복해서 적어두겠습니다.
출처 : https://steemit.com/coinkorea/@koreauniv/markowitz-modeling-for-cryptocurrency
투자 0순위 : 비트코인
코인시장에만 자산을 쏟고 있는 투자자라면, 위험분산을 위해 어떻게든 비트코인의 비중을 최대한 높여야 합니다.
투자 1순위 : 이더리움 + 리플(혹은 대쉬나 바이트코인)
그 외의 그나마 안정적인 수익률을 유지하기 위해서는 이더리움에 무게를 두고, 다른 코인들과 상관관계가 적은 알트코인에 투자해야 합니다.
투자 2순위 : 피어코인 or 네임코인 등 파생화폐
비트코인과 거의 비슷한 기술로 개발되어 파생화폐라 불리는 녀석들은 비트코인에 투자하고 싶지 않을 때 대체재로서 적절합니다.
투자 3순위 : 나머지 코인
가장 간단하면서도 뛰어난 효과를 볼 수 있는 방법, 각 코인에 대해 1/n 만큼 분산투자를 합니다.
또한, 수수료를 감안하여 리밸런싱의 주기는 최소 1주일에서 길게는 한 달 정도로 두는 것을 추천드립니다.
마치며
워렌버핏은 원수에게 파생상품을 가르치라는 말을 남겼습니다. 대신에, 저는 원수에게 코인시장을 가르치라는 말을 하고 싶습니다. 주식시장에 비해 터무니 없이 문턱이 낮으면서, 공매도 마진거래 등 일확천금을 할 수 있을 것만 같은 착각을 주고, 시장은 24시간 내내 돌아가며 사람의 영혼을 빼놓기 딱 좋습니다. 흔하디 흔한 환헷지(환율 변동분에 대한 보험 등 대처)조차 안 되는 시장이며, 거래소의 양아치 행보와 먹튀에 대한 불안감도 계속 커지고 있습니다.
스스로에게 계속 의문을 가져보면서 투자에 임하시기 바랍니다.
나는 과연 투자에 적합한 사람인가? 투자가 아니라 도박을 하고 있는 것은 아닌가?
오늘도 많이 배워갑니다 감사합니다! 업봇드리고 갑니다 :)
히히히 감사합니다!
저를 웬수로 아는 분이 있기는 합니다. 제가 가르켜드린 분의 사모님께서
ㅋㅠㅠㅠㅠㅠㅠㅠ 저도 그래서 주위에 절대 얘기 안하고 다닙니다
좋은 글 감사합니다.
좋게 봐주셔서 감사합니다!
글쎄요.. 섀넌 포트폴리오 솔직히.. 특정 모형에서만 이론처럼 이상적인 그래프가 나오는것이고.. 현실에서는 좀 다른 것 같은데요.. 결국엔 수익률 반 포기하니까 손실도 반이 줄어든것인데.. 그냥 거래횟수를 2배 줄이는게 더 좋아보이겠어요..