I will briefly introduce the main idea of the cut algorithm for Bayesian analysis. It is part of my PhD notes, hope you enjoy!
这篇短文将简短的介绍贝叶斯分析中的修剪算法,是我PhD研究中的一些简要笔记,望点赞支持~
We know that Bayesian analysis is popular in modern statistical analysis because (1). it allows simultaneous incorporation of all relevant data. (2). it simultaneously deals with all uncertainties in a single big model. Bayesian model can be divided into some smaller sub-models and we call it modules. However, there is always case that we can not guaranty our assumption on each module is correct. The reliability of the whole model may be affected given some modules are not correctly specified. This motivates us to modularize the whole model and the cut algorithm is proposed to prevent good modules being contaminated by suspect modules.
贝叶斯分析是统计学中一种非常流行的方法,因为它可以同步分析多个数据源,并且可以用一个大模型来同步考虑所有的不确定性。贝叶斯模型可以分解成许多个子模型。然而我们很难保证每一个子模型的统计假设都是正确的,模型整体的可靠性会因为部分子模型的错误假设而降低,修剪算法的目的就在于将这种错误假设导致的不良影响尽可能的局部化,以降低这些不良影响对整体模型的影响。
Consider this simplified example, we assume data Z depends on the parameter φ and data Y depends on both φ and θ, the joint distribution is:
考虑如下的例子,我们假设Z基于参数φ并且Y基于参数φ和θ,联合分布如下:
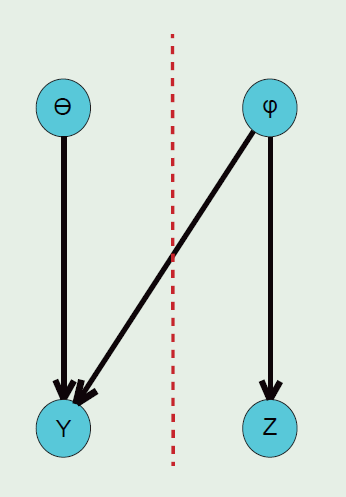
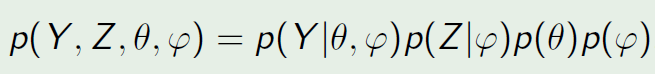
We can write its posterior and we can see that the estimation of φ depends on both Z and Y. Imaging we are confident about the specification of Z but not Y.
我们可以写出它的后验分布并且我们可以看到对于参数φ的估计是基于数据Z和Y的。假设我们充分信任数据Z的统计假设但是不信任Y。
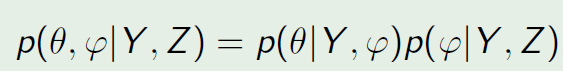
The misspecification on Y may affect the estimation of φ, we modify the posterior to the cut distribution to cut this possible bad effect. So the only difference here is the estimation of φ no longer depends on Y.
对于数据Y的错误统计假设可能影响φ的估计,我们将原来的后验分布修改成新的修剪分布,这样可以将不良影响消除。修改后的修剪分布同原来的后验分布的唯一区别在于参数 φ的估计不再依赖于数据Y。
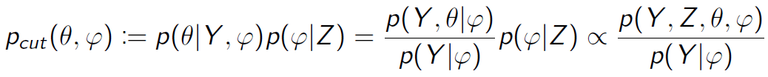
However, we have a problem if we use the naive cut algorithm to draw samples from the cut distribution. This algorithm uses two transition kernels to draw φ and θ separately.
然而,利用修剪算法来从修剪分布生成样本是有问题的。这个算法利用两个转移核函数来分别生成参数φ和θ的样本。
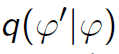
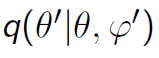
The previous study has pointed out that the Markov chain does not have the cut distribution as its stationary distribution. Instead, there is a weight function.
以前的研究指出这种生成样本的方法会导致生成的马氏链的稳态分布不是作为目标的修剪分布。相反,会产生一个额外的权函数。
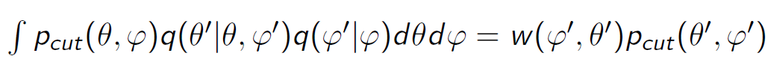
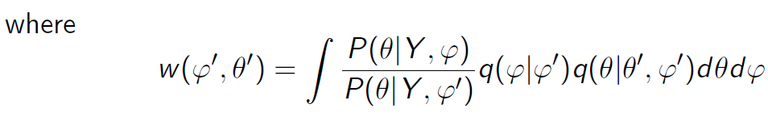
I will introduce how to make this weight function be 1 in next post.
下一篇文章会介绍如何使这个多余的权函数变为1。
Reference:
参考文献:
Plummer, M. (2015). Cuts in Bayesian graphical models. Statistics and Computing, 25(1):37{43.
注:图片自制
Sponsored ( Powered by dclick )
[DCLICK HTML Ad] - Earn Steem from your blog or website!
Hi Steemians. Today, I'd like to introduce you to th...

This posting was written via
dclick the Ads platform based on Steem Blockchain.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Congratulations @epi5tat! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @epi5tat!
Your post was mentioned in the Steem Hit Parade for newcomers in the following category:
I also upvoted your post to increase its reward
If you like my work to promote newcomers and give them more visibility on the Steem blockchain, consider to vote for my witness!