0 引言
缺乏隐私保护是比特币系统的主要缺陷之一,比特币网络中的所有交易以明文的方式记录在区块链上。虽然比特币系统使用的是与身份无关的地址,通过追踪货币在地址之间的流动,依然可以分析出来哪些地址属于同一个用户。在BTC基础上增加匿名性、部署零知识证明成为衍生币种的主要技术路线之一。
-2015年提出的 Zerocash使用了一种特殊类型的零知识证明工具 zk-SNARKs 实现了对交易金额与交易方的完全隐藏。
-2017 年,Zerocash 团队提出了将 zk-SNARKs 与智能合约结合的方案,使零知识证明 zk-SNARKs 获得了更高的关注度。
-2018年以太坊在"大都会"分叉最大和最重要的特性就是执行 zk-SNARKs。
那么零知识证明及zk-SNARKs是什么?
图片: 
zk-SNARKs 全称 Zero-Knowledge Succinct Non-Interactive Argument of Knowledge,即"简明非交互零知识证明"。zk-SNARKs 基于"零知识证明"(zero knowledge proof,即ZKP)。
1、零知识证明的概念
故事1:
早在16世纪的文艺复兴时期,意大利有两位数学家为竞争一元三次方程求根公式发现者的桂冠,就采用了零知识证明的方法。当时,数学家塔尔塔里雅和菲奥都宣称自己掌握了这个求根公式,为了证明自己没有说谎,又不把公式的具体内容公布出来,他们摆开了擂台:双方各出30个一元三次方程给对方解,谁能全部解出,就说明谁掌握了这个公式。比赛结果显示,塔尔塔里雅解出了菲奥出的全部30个方程,而菲奥一个也解不出。于是人们相信塔尔塔里雅是一元三次方程求根公式的真正发现者,虽然当时除了塔尔塔里雅外,谁也不知道这个公式到底是个什么样子。从这个故事,我们可以初步了解零知识证明的概念。
交互的消息能构成一个证明(仍然体现了传统证明的精髓)而它们本身不泄漏“断言为真”之外的任何知识。这里的“知识”可以理解为“计算能力”,证明是“零知识的”意味着整个证明过程没有增加验证者的计算能力(即验证者之前无法解决的问题在证明完成之后仍然无法解决)。这个性质保证了交互完成后验证者只知道被证明的断言为真,但他并不知道怎么转而向其他人证明这一断言,它的代价是会产生一些微小的错误。
所以,零知识证明的本质就是在不揭晓我所知道或拥有的某样东西的前提下,向别人证明我有很大几率(这点很重要,零知识证明说到底是一个概率上的证明)确实知道或拥有这个东西。
"零知识证明"能够成立必须具备以下三个要素:
•完整性:如果声明为真,那么一个诚实的验证者可以被诚实的证明者相信;
•可靠性:如果声明为假,不排除有一定概率欺骗者可以说服诚实的验证者它是真的;
•零知识:如果声明为真,那么验证者在证明过程中并不知道任何关于声明的消息。
故事2:
这里一个比较精确一点的例子就是向红绿色盲来证明两个球着色不同(一个红一个绿,见这里):视觉正常的证明者持有的传统证明/证据是眼里看到的不同颜色,他先将两个球分别放在色盲的两只手中,记住左右手中的颜色;色盲将手放背后,脑子里随机决定是否在背后交换手中的球,然后将双手握球展示给证明者并问他自己是否刚才在背后交换了手中的球,证明者通过对比之前色盲两手中球的颜色来回答他的问题。这一交互证明体现了上述传统证明系统的两点精髓,对于第二点, 这里带来了1/2的错误概率,即对于错误的断言(即两个球颜色相同),证明者仍能以1/2的概率骗过验证者,不过这可以重复多次来降低这一概率。零知识在这里显而易见:色盲在交互结束后除了相信他手中球是颜色不同的之外并没有得到任何额外的知识。
2、零知识证明的应用
从1985年零知识证明被首次提出,到今天已经是重要的密码学基础构件。但是在很长一段时间内,零知识证明协议由于没有较好的运行效率和通用性,只是停留在理论。这些理论的零知识证明协议具有不同的特点。有的协议是专职的,只能证明某些特定的事情,比如,图同构问题。有些零知识证明协议是全能的,只要你能用代码定义的问题,它都能证明(只是理论可行,不意味着有运行效率)。有些协议是交互式的,需要证明者和验证者来回发很多轮消息,有些是非交互式的,证明者只需要根据协议向验证者发一次消息。有的协议证明大小与问题规模相关,问题越复杂,证明越长。而有些协议下,无论问题多复杂,证明大小都一样。而一个全能的,非交互的,常数大小的零知识证明协议,是密码学研究者们多年奋斗的目标。
到目前为止,具有应用前景的零知识证明工具可以分为两类,一类证明慢、验证快、证明体积小,另一类证明快、验证快、证明体积大。第一类由于验证快,不占用空间的特点,得到了区块链开发者的青睐,随着Zcash而闻名,其代表协议 zk-SNARKs 还有社区开发的 C++ 库。第二类证明快的特点使得其在移动设备,嵌入式设备的部署成为可能,而隔离见证等技术有望缓解其证明体积较大的问题,在区块链领域的也是前途无量。
图片: 
3、零知识证明与数字货币
2015年提出的 Zcash最早将零知识证明运用到数字货币的隐私性中。一般数字货币领域中说的零知识证明实际上指zk-SNARKs ,即"简明非交互零知识证明"。BCH和ETH都是努力将zk-SNARKs运用到代币领域的典范。下面援引知乎(DENG、高超峰等)上关于Zcash运用零知识证明与比特币区别的解释:
举例对象依然是数字货币界最著名CP:Alice和Bob。
一、从比特币说起
直接讲解ZCash的交易过程可能会比较抽象。为了有助于理解,我们不妨先分析比特币,作为铺垫。
我们先来打个比方说明比特币的转账原理。
演示场景:Alice转1个比特币给Bob。
转账前,Alice要事先准备1个比特币。为了方便理解,我们把Alice准备转出的这1个比特币看成一张面额为1个比特币的“支票”,如图1。
图1
从这张“支票”中我们可以获取到如下信息:
图片: 
Alice确实拥有1个BTCAlice使用私钥对这张支票签名,证明Alice拥有对这笔资产转账的权力。
支票的面额和转账权都已经明确,Alice就可以给Bob转账了。转账的原理很简单,就
是给Bob新建一张一样的“支票”,证明Bob拥有了1个比特币。同时撕掉Alice手中那张的“支票”,通过这“破旧”并“立新”的方式,实现资产所有权的转移。如图2。
图2
以上逻辑其实不难理解,因为这和日常生活中的银行转账是一个道理。通过银行转账,我们在交易时不必对实物货币进行转移,而是以银行记账的方式,实现“资产所有权”的转移。比特币交易的过程实质上就是一个“资产所有权”的转移过程,转入比特币的那一方“新建”一份资产所有权,而转出方需要“销毁”原先的资产所有权,被销毁的那张“支票”永远不会再出现。
二、ZCash的转账原理
图片: 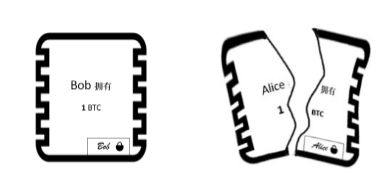
与比特币一样,ZCash的交易过程也是 “资产所有权”的转移。继续沿用前文“支票”的比方。
演示场景:Alice转1个ZEC给Bob。
转账前,Alice创建一张面额为1个ZEC的“支票”,如图3。
图3
能从该凭证中获取的信息:
图片: 
Alice确实拥有1个ZEC。Alice使用私钥对这张支票签名,证明Alice拥有对这笔资产转账的权力。这张“凭证”上多了一串随机数,用符号 r 表示。这串随机数的作用好比 “支票代号”,用来唯一识别该支票。Alice的“支票代号”为r1。
明确以上信息,Alice就可以进行ZEC转账了。
第一步:比特币一样,要先为Bob新建一张“支票”。Bob的支票代号(r2)与Alice的支
票代号(r1)不相同,如图4。
图4
第二步:新的“资产所有权”生成的同时,必须要想办法销毁原来的“资产所有权”。即必须想办法让Alice手中的“支票”失效。与比特币简单粗暴的“直接撕毁”不同,ZCash采用“备注作废”的手段,达到同样的效果。怎么理解呢?就是在不对原先“支票”作任何处理的前提下,新建一个作废文件列表,录入需要作废的“发票代号”。如图5,
图5
从上图可以看出,原先的Alice持有的支票仍旧存在,并没有消失,只是这张支票已经被记入“作废列表”。在确定资产所有权时要同时读取两个列表的信息,能确定Bob拥有资产所有权的判断方法是:作废列表中不存在Bob所持“支票”的代号。
可是为什么要这样设计呢?其实这样设计的目的是为了在交易过程中运用 “零知识证明”。
Alice要向Bob转一个单位的数字货币(BTC/ZEC),即Alice要向Bob转移一个单位的资产所有权。这时有以下两个方法:
图片: 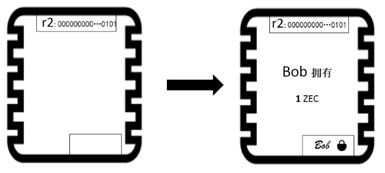 图片:
图片: 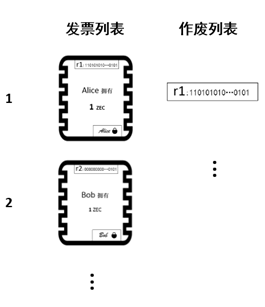
(一)比特币中的做法:Alice拥有一张1BTC的支票,要转账给Bob时,先给Bob新建一张1BTC的支票,同时当着Bob的面将自己原先的支票撕毁。
(二)ZCash中的做法:Alice拥有一张1ZEC的支票,要转账给Bob时,先给Bob新建一张1ZEC的支票,然后在一张约定有效的作废列表中,记录下Alice的发票的代号,证明Alice的支票已经失效。
ZCash的方法属于零知识证明。整个交易过程中,Bob并没有见过Alice的支票,但是还是实现了资产所有权的转移。在ZCash的整个交易系统中,Alice和Bob的交易还有其他见证者,即负责记录交易信息的矿工。同样道理,每笔交易矿工能接收到的东西只有一个发票代号,和一张新的发票,而且这两样东西都是被加密的。所以矿工并不知道转账双方是谁,也不知道转账金额是多少。
4、zk-SNARKs 的工作原理
zk-SNARKs 由3种算法组成:G、P、V。
G是一个密钥生成器,需要通过生成随机变量 L(必须保证任何情况下不能泄露)和程序C。然后生成两个公钥——证明公钥 Pk 和验证公钥 Vk ,这两个公钥都是公开的,任何人都可以查看。
P是证明者,需要输入三个参数,即证明公钥 Pk、公开的随机输入散列值 x 以及需要证明的隐私声明 w 。P 算法生成证明 prf ,函数表达为:prf = P ( Pk , x , w )
V 作为验证者将会返回一个布尔类型的结果,即 true 或者 false 。V 将验证公钥 Vk 、P 中的随机输入散列值 x 以及证明 prf 作为输入参数进行验证,即 V ( Vk , x , prf ) 。如果证明者正确,返回 true ,否则返回 false 。
由以上 G、P、V 三者的关系可以看出,随机变量 L 至关重要,必须保密。因为任何人都可以用它来生成假的证明,这些假的证明也能返回 true ,而不管证明者是否拥有隐私声明 w 的知识。
下面让我们继续回到我们的老朋友 Alice 和 Bob 的身上,Alice 是证明者,Bob 是验证者。
Bob 作为验证者第一件事就是要使用 G 生成证明公钥 Pk 和验证公钥 Vk ,为此他需要生成随机变量 L,正如上面提到的,Bob 对 L 必须非常小心,他不能让 Alice 知道 L 的价值以防 Alice制造假的证明。
既然 Bob 生成了两个公钥,Alice 需要生成证明 prf 来证明声明的有效性。她将使用证明算法 P 生成证明,来证明她知道隐私声明 w 的哈希值为 x 。接下来 Alice 将把这些证明参数交给最终运行 zk-SNARKs 验证算法的 Bob 。Bob 将会使用验证算法 V (Vk , x , prf)来验证结果,如果返回 true ,则 Alice 很真诚,确实知道隐私声明 w 是什么。如果返回 false ,则 Alice 在说谎她知道 w 是什么。
5、附注:网上广泛流传的错误的例子
证明举例(来自百度百科等)
A要向B证明自己拥有某个房间的钥匙,假设该房间只能用钥匙打开锁,而其他任何方法都打不开。这时有2个方法:
①A把钥匙出示给B,B用这把钥匙打开该房间的锁,从而证明A拥有该房间的正确的钥匙。②B确定该房间内有某一物体,A用自己拥有的钥匙打开该房间的门,然后把物体拿出来出示给B,从而证明自己确实拥有该房间的钥匙。
后面的②方法属于零知识证明。好处在于在整个证明的过程中,B始终不能看到钥匙的样子,从而避免了钥匙的泄露。
这个例子是谬误。上面证明A拥有房间钥匙的方法显然不是零知识的,考虑一个不诚实的验证者B,他不知道房间里有些什么,但他可以要求A“请把房间里外套拿出来”,如果A拿出来了,B立即知道了原来房间里还有件外套,这是B在证明之前所不知道的。
参考资料:
[1]zcash官网https://z.cash/
[2]知乎专题零知识证明(DENG、高超峰等)
[3]以太坊官网https://www.ethereum.org/
[4]V神解释零知识证明,https://medium.com/@VitalikButerin?source=post_header_lockup
欢迎大家关注公众号:区块狂热
Run by Wesley&Tintin
微信扫描下方二维码关注我们

谢谢分享!
讲的是“零知识”,读得的知识大于零。🙏
有人阅读是最大的褒奖
复杂,看得头晕。坚持看完,感觉还是有收获的,谢谢你的分享
Posted using Partiko Android