There are two ways to design and solve related fluid flow engineering systems, through experiment and calculus. Experiment refers to the point of building and testing models and prototypes while calculus refers to solving the differential equations that govern the problem. We use CFD to get what we could get if we did all the models we need to do to solve the problem. Yet Experiments are an important part because they’re used to validate the simulation experiment. I'm going to explain you about geometry and the mesh.
Geometry
When facing a CFD problem, one thing that one must do is to have defined as detailed as possible the complete domain that is involved. It is very important to know what data is required to take from the domain and where is used. It could happen that you just need to solve certain equations in a section of your domain problem, and just a few in other part. So simulating all the domain in the same simulation with all equations can result in wasted time and computational resources.
This brings the next important step, how is the shape of the domains to simulate? Dividing the problem in several simulations reduces a bit the computational time but what really reduces it is the size and number of elements of the mesh, and that can be achieved if we reduce the domains and simplify as much as possible.
For example, let us imagine a fluid flowing inside a long tube, this tube is absorbing heat at certain heat flux and is transmitting it to the fluid flowing inside, people can find themselves tempted to create the 3D volume inside the pipe and try to simulate the whole domain of it to get some exact results. However, this results in overloading the simulation with unnecessary elements. One of the best way to go is to simulate a 2D axisymmetrical model with cylindrical coordinates, that way we can solve the problem “in a small piece” of the body and get the result of the whole domain. This brings two benefits, shorter simulations times and better quality of meshes. If it’s necessary to do the 3D body, for example the same volume inside a pipe, one-way to simplify is to section the body in fractions, like a half, a quarter, etc. (as see below)

Mesh
The mesh is a series of blocks or cells that form the volume to study. The mesh is one of the most important part of the simulation, and if done badly, can cause many problems. The mesh is the representation of the volume of the simulation and it must have all the walls and solid bodies it is in contact. Many factors influence in the quality and precision of results. Two important factors of the mesh are the quality and the skewness.
The mesh can be structured or unstructured. The structured mesh uses plain cells with four sides (if 2D) or six faced volumes (3D) and tries to follow a uniform pattern. If is unstructured it can have two types of elements, triangles and quadrilaterals (if 2D) or tetrahedrons (3 edges) and hexahedrons (cubes) and does not follow a pattern in the elements distribution, like same spacing or size. Usually with an unstructured mesh you end with more elements than with a structured mesh.

Tetrahedrons in a cylinder
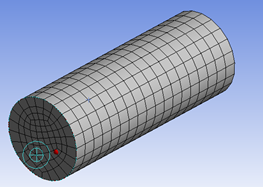
hexahedrons in a cylinder.
The skewness is a way to measure how the distortion in the elements of the mesh is. It checks how the angles of the edges are. The skewness can be cero if for example the 2D element is a perfect square or rectangle with all 90° angles or if the triangle is equilateral (all 60°), in 3D, all the faces must be perfect squares or perfect triangles.
When you face complex geometry, it is recommended to try to generate blocks in such a way that the skewness is small as possible in all the cells. With complex geometries it is needed a hybrid mesh, this combines regions of unstructured and structured blocks. In the example of the cylinder, and if it’s needed to use a 3D model, a hybrid mesh is the best option to go, as it allows to generate a mesh with high resolution near the walls.
Some forms of meshes are popular because they are the best options for certain geometries. For example, for 3D cylinders, O-grids are necessary; they have low skewness and it allows the creation of denser sections near the walls. Airfoils /NACA profiles are recommended to be simulated with C-grids, which divide the domain in a C and a rectangle.
When facing geometries with spike-ends, one solution is to try to cut it near the spike and to create cells that can have low skewness near this area. Sometimes creating the mesh consumes a lot of time, but this time can be nothing in contrast with all the time wasted with simulations with poor/ not confinable results. Finer meshes does not mean better results or higher quality, in some cases it does, but it’s not common. Finer cells or high density of the mesh are always needed near walls or bodies so the viscous effects can be properly calculated.
For example, fluent allows you to check the quality and the skewness of the mesh. When using 2D meshes try to achieve a high quality, near 95% is good. With 3D meshes, it is different; some meshes can achieve convergence with a 40%, but is recommended to get more than 70%. And skewness, as low as possibly as it will get you convergence problems, especially in turbulent flows.
Congratulations @sarien! You received a personal award!
Happy Birthday! - You are on the Steem blockchain for 1 year!
Click here to view your Board
Congratulations @sarien! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!