파레토 법칙과 블록체인
파레토 법칙이란 프랑스 경제학자이자 사회학자인 Vilfredo Federico Damasso Pareto가 유럽제국을 조사하여 얻은 소득분포에 관한 통계적 법칙으로서 흔히 8:2의 법칙으로 불린다. 8:2의 법칙은 ‘상위 20%의 사람들이 전체 부의 80%를 갖게 된다.’라는 보다 직설적인 의미로도 해석이 가능하지만, 시대가 변화함에 따라 파레토 법칙은 소수의 사람들이 부, 명예, 자원 등 으로 나타나는 ‘힘'의 대부분을 갖게 되는 사회적 현상을 포괄하는 개념으로 사용되고 있다.
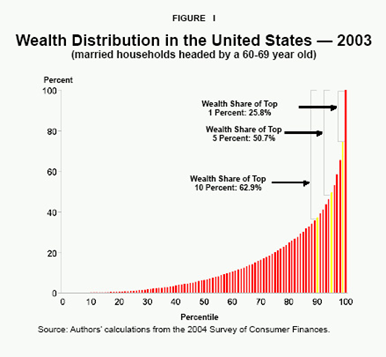
파레토의 8:2 개념을 좀 더 심화한 영국의 물리학자 Derek J. de Solla Price의 제곱근의 법칙에 따르면 생산활동이 존재하는 인간 사회의 다양한 분야에서 전체 생산량의 절반은 참여자 수의 제곱근에 해당하는 수의 사람들에 의해 생산 된다. 예를 들어 특정 과학 분야에서 연간 출고되는 100편의 논문이 총 25명에 의해 쓰여졌다면 이 중의 반에 해당하는 50편의 논문은 25의 제곱근 즉 대략 5명에 의해 쓰여진다는 것을 의미한다. 연간 쓰여지는 논문의 수 , 매년 작곡되어 출시되는 음원의 수, 매년 출간되는 책의 수, 심지어 축구 경기에서 들어간 골의 수 까지, productive domain, 즉 생산이 존재하는 분야 어디든 소수의 그룹이 매우 큰 부분의 결과를 좌지우지 한 다는 것이다.
그렇다면 현재 블록체인 생태계는 어떨까? 블록체인 기술과 뗄래야 뗄 수 없는 매우 큰 이슈는 바로 ‘분산화' 이다. 중앙통제 없이 누구나 사용가능한 네트워크를 추구하는 블록체인 기술의 최초 적용 사례인 비트코인의 경우는 ‘중앙통제’가 완전히 존재하지 않는다고 할 수 있을까? 실제로 비트코인 내에서 블록을 생성하고 블록 내에 다양한 사람들의 거래를 기록을 하는 매우 중추적인 역할의 수행자는 바로 ‘채굴자'이다. 이들에게도 앞서 설명한 파레토 법칙과 프라이스 법칙이 적용될 수 있을까?
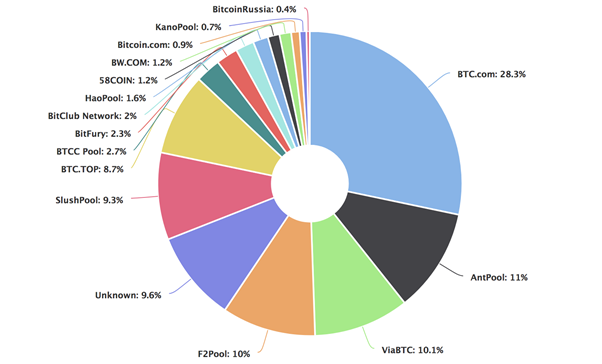
2018년 4월 29일 UTC +9hr (한국 시간) 오후 9시 15분 기준 https://blockchain.info/pools 에 나타나는 비트코인 네트워크 내 블록 채굴 파워(hash power)로 분류한 도표를 살펴 보자. 비트코인 전체 네트워크의 블록 채굴 파워 상위 16개 중의 채굴 풀 중 4개의 채굴 풀이 전체 네트워크 채굴 파워의 50% 이상을 점유하는 것을 쉽게 확인 할 수 있다. 상위 16개의 제곱근에 해당하는 수의 채굴 풀이 전체 파워의 반 이상을 점유하는 것은 프라이스의 제곱근 법칙에 정확히 부합하는 것을 알 수 있다.
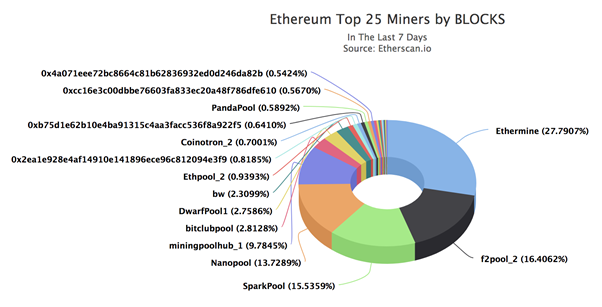
비트코인 다음으로 큰 시장을 형성하고 있는 이더리움 의 경우는 어떨까? 이더리움의 경우 상위 25위 채굴 풀 중 3개의 채굴 풀이 50% 이상의 블록 채굴 파워를 보유하고 있다. 25의 제곱근에 해당하는 상위 5개의 채굴 풀은 무려 상위 25 채굴 풀의 채굴 파워 중 80%를 차지하고 있다. 하지만 상위 5개의 채굴 풀이 아닌 25개의 채굴 풀 중 5개의 채굴 풀, 즉 이 경우 가장 큰 부분을 차지하는 Ethermine을 제외한 f2pool, SparkPool, Nanopool, miningpoolhub_1, bitclubpool이 50%이상의 채굴 파워를 보유하는 것을 확인할 수 있다. 흥미롭게도 이더리움 네트워크의 경우 파레토의 8:2의 법칙역시 정확히 부합하는 것을 확인할 수 있다. 상위 25개의 20%인 5개의 채굴 풀은 네트워크 전체의 80% 블록 채굴 파워를 점유하고 있는 것을 확인 할 수있다.
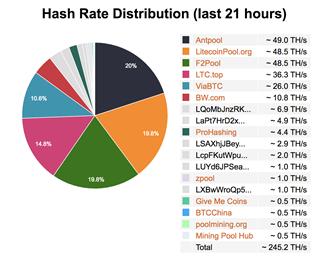
그렇다면 시가총액 7위의 라이트 코인의 블록체인 네트워크는 어떨까? 라이트 코인 네트워크의 경우 상위 18개의 채굴 풀 중 상위 3개의 채굴 풀이 네트워크 전체 블록 생성 파워 중 50%이상을 장악하고 있다. 18의 제곱근인 4.24, 즉 18개의 채굴 풀 중 4-5개의 채굴 풀(Antpool, F2Pool, LTC.top, ViaBTC, BW.com)이 네트워크 전체 블록 생성 파워 중 50%를 차지하고 있으며 이는 프라이스의 제곱근 법칙에 부합하는 것을 확인할 수 있다.
블록 생성 파워 또는 해쉬 파워로 상징되는 네트워크 내의 영향력은 조사된 모든 샘플 블록체인 네트워크 내에서 서로 약속이라도 한 것 처럼 프라이스 법칙 혹은 파레토 법칙에 부합하는 것을 확인 할 수 있다. 소득분포의 통계적 조사로 시작된 파레토의 8:2 법칙 그리고 이를 scientific productivity(과학적 생산성)에 접목한 프라이스 제곱근 법칙이 블록체인 세계에 시사하는 바는 무엇일까?
우선 가장 직접적이고 확실한 진단은 현재 많은 사람들이 열광하는 1세대 블록체인, 즉 PoW 기반의 블록체인 네트워크는 수 많은 참여자들이 모여 각 네트워크의 커다란 유기체를 구성 하고 있으며 네트워크의 중추적인 역할을 하는 채굴자들 중 소수의 채굴 풀을 중심으로 네트워크의 영향력이 집중 되어 있다는 것이다. 사람들이 블록체인 네트워크를 비판하는 이유 중 하나는 바로 ‘분산화의 실패'인데 파레토 법칙과 프라이스의 법칙이 적용되는 인간사회의 다양한 분야를 떠올려 보면 분산화 실패는 비단 블록체인 네트워크에만 국한된 문제가 아니라는 것을 알 수 있다. Top 100 음원 차트에 이름을 올리는 작곡가의 수, 영화 초반 부에 나오는 몇몇 익숙한 이름의 영화 배급사들, 그리고 국내 기업의 전체 이윤의 65%를 차지하는 국내 100대 재벌 기업들까지, 어쩌면 모든 인간의 창의적, 생산적 범주엔 매우 구조적이고 체계적인 힘의 집중이 존재 할 수 밖에 없는 것 일지도 모른다.
그렇다면 우리는 파레토 법칙과 프라이스의 법칙과 같은 ‘무자비한 통계’의 굴레에서 벗어날 수 없을까? 블록체인의 미래 역시 몇 가지의 통계적 법칙에서 자유로울 수 없는 것일까? 분명 쉽게 답 할 수 있는 문제는 아니지만 필자가 바라보는 블록체인 세계는 이제 막 생겨난 매우 독특한 유형의 소 우주에서 탄생하였다. 이 우주는 철학, 경제, 금융, 과학, 수학, 물리, 통계, 심지어 아시아 변방 마이크로네시아의 야피족 화폐문화 까지 인터넷에 존재하는 모든 지식과 문화가 매우 빠른 속도로 한데 모이고 있으며 현재 엄청난 가능성을 지닌 멜팅팟을 형성 하였다. 이 용광로에는 과거에 주목 받지 못한 다양한 지식이 재조명 되고 새로운 기술이 융합되어 인류역사상 한번도 경험하지 못한 개념의 ‘블록체인’을 세상에 선보였다.
이제 본격적으로 중량을 더하고 있는 이 소 우주는 지속적으로 블록체인의 새로운 개념적, 기술적 실험을 감행할 것이고 매우 빠른 속도로 지평을 개척해 나갈 것이다. 현재 파레토 법칙과 프라이스 법칙에 정확히 부합하는 블록체인 1, 2세대의 상황은 마치 산업 혁명기에 대량 생산 체계가 낳은 새로운 부의 탄생과 극단적인 부의 비대칭, 그리고 이러한 자본주의적 궤를 함께 하는 현재 2018년 대한민국 100대 기업의 경제력 집중과 매우 닮아 있다. 바로 이를 극복하는 것이 블록체인 세계가 직면한 궁극의 도전일 것이며 앞으로 추가 연재를 통해 필자가 바라보는 블록체인의 미래에 대해 자세히 논의해 볼 것이다. 다음 연재에선 파레토 법칙과 대조되는 ‘롱테일’에 대해 알아보고 정보의 무한 유통으로 가능해진 개개인의 수요에 부합하는 서비스 구현, 그리고 이러한 고찰이 서비스 중심, 어플리케이션 기반 블록체인 설계에 어떠한 의미를 갖게 되는지 알아볼 것이다.
Juno Yu
IBCT
http://ibct.io/
http://blog.ibct.io/
2018.6.27
Reference:
Derek J. de Solla Price
https://en.wikipedia.org/wiki/Derek_J._de_Solla_Price
https://blog.naver.com/kambly/40013939121Pareto Distribution and Scientific productivity by de solla price, Jordan Peterson. Youtube
Pareto Distributin
https://subversion.american.edu/aisaac/notes/pareto-distribution.pdf장하성: 왜 분노하지 않는가? micimpact. Youtube
Jordan Peterson on Wealth Concentration & Normal vs Pareto Distributions. Youtube
다음글이 기다려지네요.
좋은 글 감사합니다.
잘보고갑니다
다음 편도 기대하겠습니다
감사합니다
이익이 되는 모든 분야에 적용되는군요..
정말 전문적 지식이 녹아 있는 글이네요
좋은 글 감사합니다.
Congratulations @junoyu! You received a personal award!
Click here to view your Board
Congratulations @junoyu! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!