This article is part of a series and focuses specifically on clarification of the Merkle Tree.

So what is a Merkle Tree?

In cryptography and computer science, a hash tree or Merkle tree is a tree in which every leaf node is labelled with the hash of a data block and every non-leaf node is labelled with the cryptographic hash of the labels of its child nodes.

Hash trees allow efficient and secure verification of the contents of large data structures.

Demonstrating that a leaf node is a part of a given binary hash tree requires computing a number of hashes proportional to the logarithm of the number of leaf nodes of the tree; this contrasts with hash lists, where the number is proportional to the number of leaf nodes itself.

The concept of hash trees is named after Ralph Merkle who patented it in 1979.

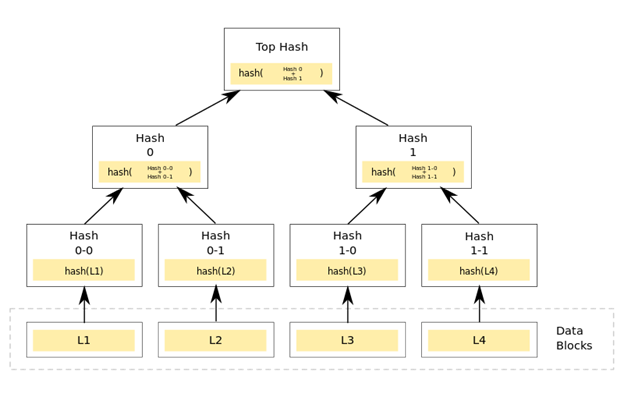
A hash tree is a tree of hashes in which the leaves are hashes of data blocks in, for instance, a file or set of files. Nodes further up in the tree are the hashes of their respective children. For example, in the picture hash 0 is the result of hashing the concatenation of hash 0-0 and hash 0-1. That is, hash 0 = hash( hash 0-0 + hash 0-1 ) where + denotes concatenation.

Most hash tree implementations are binary (two child nodes under each node) but they can just as well use many more child nodes under each node.

Usually, a cryptographic hash function such as SHA-2 is used for the hashing.

In the top of a hash tree there is a top hash (or root hash or master hash). Before downloading a file on a p2p network, in most cases the top hash is acquired from a trusted source, the genesis block. When the top hash is available, the hash tree can be received from any non-trusted source, like any peer in the p2p network. Then, the received hash tree is checked against the trusted top hash, and if the hash tree is damaged or fake, another hash tree from another source will be tried until the program finds one that matches the top hash.

The main difference from a hash list is that one branch of the hash tree can be downloaded at a time and the integrity of each branch can be checked immediately, even though the whole tree is not available yet.

For example, in the picture, the integrity of data block 2 can be verified immediately if the tree already contains hash 0-0 and hash 1 by hashing the data block and iteratively combining the result with hash 0-0 and then hash 1 and finally comparing the result with the top hash. Similarly, the integrity of data block 3 can be verified if the tree already has hash 1-1 and hash 0.

This can be an advantage since it is efficient to split files up in very small data blocks so that only small blocks have to be re-downloaded if they get damaged. If the hashed file is very big, such a hash tree or hash list becomes fairly big. But if it is a tree, one small branch can be downloaded quickly, the integrity of the branch can be checked, and then the downloading of data blocks can start.

In case of a Cryptocurrency – Disk Space Management

Once the latest transaction in a coin is buried under enough blocks, the spent transactions before can be discarded to save disk space. To facilitate this without breaking the block’s hash, transactions are hashed in a Merkle Tree, with only the root included in the block’s hash. Old blocks can then be compacted by stubbing off branches of the tree. The interior hashes do not need to be stored in case of cryptocurrencies.

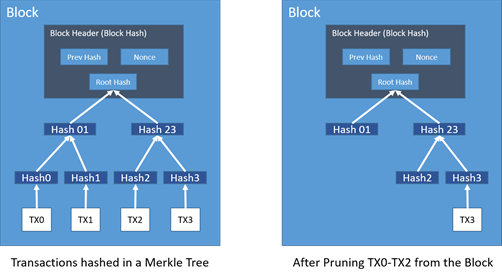
A block header with no transactions is about 80 bytes, if we take the bitcoin example where blocks are generated every 10 minutes, this equates to 80 (bytes) * 6 (blocks) * 24 (hours) * 365 (days) = 4.2MB per year.

With computer systems typically selling 2GB of RAM (as of 2008) and Moore’s Law predicting growth of 1.2GB per year, storage should not pose any problems even if the block headers must be kept in memory of the nodes.

Simplified Transaction Verification

It is possible to verify payments without running a full network node. A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he's convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it's timestamped in. He can't check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it, and blocks added after it further confirm the network has accepted it.

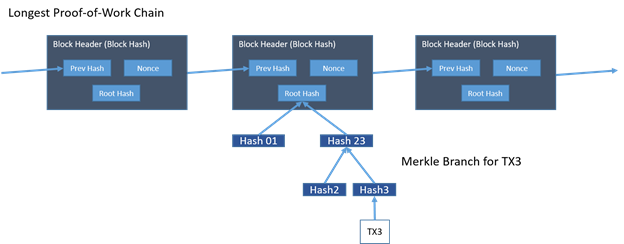
As such, the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is overpowered by an attacker.

While network nodes can verify transactions for themselves, the simplified method can be fooled by an attacker's fabricated transactions for as long as the attacker can continue to overpower the network.

One strategy to protect against this is to accept alerts from network nodes when they detect an invalid block, prompting the user's software to download the full block and alerted transactions to confirm the inconsistency. Businesses that receive frequent payments will still want to run their own nodes for more independent security and quicker verification.

That's it in a nutshell, most of this clarification is derived from Sathoshi's whitepaper, please see the link below.

Acknowledgements / References

Artwork:

• Title page “Intelligent Solutions” courtesy of http://www.hloom.com/cover-pages/
• Page header / footer “Abstract blue lights” created by Kotkoa - Freepik.com

Other references:

• https://www.coindesk.com/short-guide-blockchain-consensus-protocols/
• https://www.lifewire.com/cryptographic-hash-function-2625832
• https://en.wikipedia.org/wiki/Merkle_tree
• https://bitcoin.org/bitcoin.pdf

Contact me

You can contact me here with any questions, suggestions and / or to discuss the topic of this document:

LinkedIn: https://www.linkedin.com/in/iwanspillebeen/
CryptoPub: https://thecrypto.pub/u/iwan.spillebeen

Sponsoring

I write these papers to - hopefully - help make blockchain more accessible to people new to the technology, I don't get paid, nor sponsored to write these papers. If you absolutely feel inclined to donate something to the writing of this document, you can do so at the following address:

• Ethereum / Ether: 0x6E2a1f9baD495B894A2c6F8240918620F899f4E2

Disclaimer

Blockchain – Decrypted is written as a series of chapters, aimed at demystifying the various workings of blockchain technology. Where appropriate I use examples from existing or to-be cryptocurrencies, these examples are just that, examples, and do not aim at promoting or otherwise endorsing any given cryptocurrency.

This document does not constitute legal or financial advice and I do not make any guarantees or promises as to any results that may be obtained from using my content. No one should make any investment decisions without first consulting his or her own financial advisor and conducting his or her own research and due diligence. I disclaim any and all liability in the event any information, commentary, analysis, opinions, advice and/or recommendations prove to be inaccurate, incomplete or unreliable, or result in any investment or other losses.