
A Gambling Question for Economist
If someone offers you $10 for free, or an 11% chance at winning $100, which one should you choose?

The answer mathematically is choosing the 11% chance, as (11% * $100 > 100% * $10), however Depending on your tolerance for risk, the $10 option could be better for you. The exercise is interesting because it makes you think about risk, reward, and probabilities in a mathematical way. This is a good practice in all of investing instead of just mindlessly looking at charts and arbitrary numbers, which many people do in stocks and cryptos.
Applying Risk Reward Calculation in P2P investing
A place where risk and reward is very applicable is P2P loans at Btcpop. Btcpop.co is an open market platform that lets users set their own terms, and use altcoins as collateral. This combination of the free market and customizable terms, leads to many different combinations of loans.
high % collateral ----> no collateral. high market cap altcoins ----> low market cap altcoins high APR ----> low APR. good borrowers -----> bad borrowers. long periods of time -----> short periods of time 1 payment ------> many small payments
And so on……...
This makes its quite difficult to decide between multiple listings. As you can invest a little in a risky loan with high APR, and earn the same return as investing much more in a collateralized less risky loan with low APR. It's kind of like comparing apples and oranges in some cases. So, I looked at this dilemma like the economist gambling problem and used some risk reward calculation to compare the loans at Btcpop on a more level playing field.
Below I randomly took a screenshot of the available loans at the time of writing:
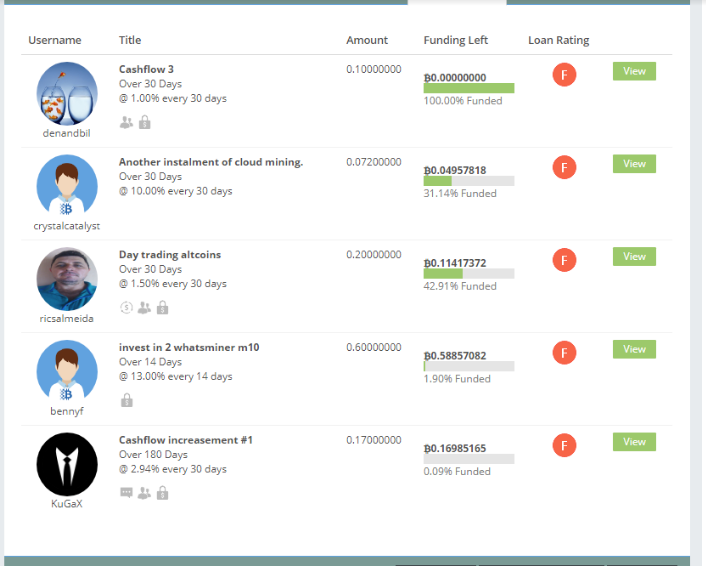 As you can tell there is quite a variety of loans. As I don’t want to fill this whole post with just screenshots of the loan information, I summarized some information inside of each loan below:
As you can tell there is quite a variety of loans. As I don’t want to fill this whole post with just screenshots of the loan information, I summarized some information inside of each loan below:
| USER | User Risk | Collateral% & (Type) | Collateral Risk | Collateral Risk Score | Reward APR |
| denandbil | 80% | 120% (ETH) | 90% | 108% | 12% |
| crystalcatalyst | 40% | 70% (LTC, variety) | 60% | 42% | 120% |
| ricsalmeida | 80% | 50% (DASH) | 70% | 35% | 18% |
| bennyf | 10% | 2% (Variety) | 30% | .06% | 156% |
| KuGax | 35% | 45% (CLAM, variety) | 40% | 18% | 35.28% |
My Calculations:
As you can see I have come up with a user risk score and summarized collateral for each user. This comes from subjective experience for calculating both the user risk and collateral risk scores. While subjective information is usually not best for objective ratings, sometimes taking long term experience and turning it into data while not perfect, can yield some very useful information.
How I calculated user risk:
Calculating user risk is a very subjective measure and is almost impossible to put an objective value on. The % roughly correlates to how likely this user is to pay back the loan without collateral. So, for reference, the owner of Btcpop who has paid back 500 BTC would be 99.9% on a 1 Btc loan. And a first time user from Nigeria would get a .1% rating for a .01 BTC loan. I calculated the score roughly based on verification, repayment history, amount of loan, age of account, and other information available on these users profiles. Again, this number is made up, but takes into account my experience and other available information.
How I Calculated Collateral Risk:
Collateral % This is a pretty straight forward measurement. It is simply the collateral value at the current market price. Collateral Risk % This takes into account the riskiness of the collateral relative to BTC (what loans are taken out in). A highly correlated liquid asset like ETH will much better track the BTC price than say small cap relatively pointless altcoin like DOGE. A common mistake people make at Btcpop is valuing all collateral at market price. This doesn’t work well, as risky altcoins price can move dramatically against the BTC price. The score roughly estimates how correlated the collateral is to BTC. So ETH gets a 90%, and DOGE gets a 30% for reference. This is subjective and my opinion, but it's based roughly on facts and experience. Reward APR The end reward of all P2P loans is interest. As the loans are different lengths the only way to compare them apples to apples is by comparing the APR of each loan. I simply listed this as a % APR.
Calculating Collateral Risk Score
In order to combine the amount of collateral with how well that collateral correlates with the Bitcoin price I came up with the Collateral risk score formula.
Collateral Risk = ((Collateral Amount) * (Collateral Risk Score))
So for the first example let's look at denandbil’s listing:
(1.2*.8) = 108%
This is a really good collateral risk score because it is positive itself. So regardless of how you feel about denandbil as a borrower, this collateral should likely be worth more than the loan unless the altcoins or Bitcoin make rapid uncorrelated price movements. If we look at crystalcatalyst for comparison, he also has a decent amount of collateral (70%) but the collateral is of lower quantity and quality than danandbil. So his collateral score is significantly lower:
(.7*.6) = 42%
Combining User Risk with Collateral Risk The next logical step is to combine collateral risk and user risk. This is a little less straightforward, as if a person has enough collateral, they are actually more likely to pay back a loan. It doesn’t really matter how trustworthy they are. On the other hand, if someone doesn’t have much collateral, their user risk score is much more important. So to do this, we will add 1 to the collateral risk score and divide it by 2. So the formula will reflect 100% collateral is neutral (1), (1+1)/2. And the formula will reward higher than 100% collateral, and punish lower than 100% collateral. This is then multiplied by the Borrower score:
((Collateral risk score) + 1)/2) * (User Risk Score) = Overall Risk Score
So for denandbil:
((1+1.08)/2) * .8 = 83.2%
This roughly means there is a 83.2% chance your risk investing in this borrower is going to end in reward Compared to crystalcatalyst
((1+.42)/2) * .4 = 28.4%
This roughly means there is a 28.4% chance your risk is going to end in reward by your subjective estimates.
| User | User Risk | Collateral /type | Collateral Risk | Collateral risk | Overall Risk | Reward APR | Risk Reward Score |
| denandbil | 80% | 120% (ETH) | 90% | 108% | 83.2% | 12% | .9321 |
| crystalcatalyst | 40% | 70% (LTC, variety) | 60% | 42% | 42% | 120% | .6248 |
| ricsalmeida | 80% | 50% (DASH) | 70% | 35% | 54% | 18% | .6372 |
| bennyf | 10% | 2% (Variety) | 30% | .06% | 53% | 156% | .1356 |
| KuGax | 35% | 45% (CLAM, variety) | 40% | 18% | 20.6% | 35.28% | .279 |
Calculating Final Risk Reward Score
So now that we have an approximate risk score, we can combine that with the reward (APR) in order to compare investments. Because our expected reward is a Percentage APR, we will calculate the value by multiplying the risk score which is roughly the likelihood of repayment by the reward to get the expected value.
(Risk Score) * (Reward) = Risk Reward Score
So for denandbil:
.832 * 1.12 = .93184
This score doesn’t necessarily mean anything specific, but the higher the score the better. As you want highest chance of repayment and the highest reward for your investment. This makes sense as the nature of investing is that the higher the risk, the higher the reward. So if you can get a lower risk and a higher reward combined, the better the investment. For comparison let's look at crystalcatalyst
.284 * 2.2 = .6248
So what this shows, is that even though the interest payment for crystalcatalyst is 10x the interest for denandbil (120% APR vs 12% APR). When you factor in how risky crystacatalyst is, denandbil is still a better investment. This equation then seemed to work well for the other investments. Scoring loans I would invest in higher, and loans I definitely would not invest in lower.
Doing this for yourself
None of this is science, but exercises like this are good for investors as it compares investments taking risk into account. Sure 120% APR sounds a lot better, but it's also more risky. And 12% APR sounds boring, but when its almost a sure thing, it's a better investment. So looking at the table again, a person using logic (and experience) can see that the score is actually pretty reflective of how good the investment is. And this is only with a few variables. This could easily be adjusted and made better. Adding more variables and more properly weighting them. Generally the more information the better, so long as you weigh the information as accurately as possible.
| User | User Risk | Collateral /type | Collateral Risk | Collateral risk | Overall Risk | Reward APR | Risk Reward Score |
| denandbil | 80% | 120% (ETH) | 90% | 108% | 83.2% | 12% | .9321 |
| crystalcatalyst | 40% | 70% (LTC, variety) | 60% | 42% | 42% | 120% | .6248 |
| ricsalmeida | 80% | 50% (DASH) | 70% | 35% | 54% | 18% | .6372 |
| bennyf | 10% | 2% (Variety) | 30% | .06% | 53% | 156% | .1356 |
| KuGax | 35% | 45% (CLAM, variety) | 40% | 18% | 20.6% | 35.28% | .279 |
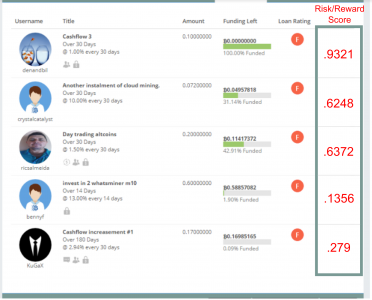 Denandbil is the highest scoring loan, and that is also why it was already funded when I took the screenshot. Investors whether they make their own crazy formula or not, can spot a good deal. The next 2 investments were better in comparison, but still had some issues. The one had a riskier borrower with 70% of decent collateral, but the other had a better borrower with 50% of a slightly better collateral. And the last 2 investments, in my opinion, were inadvisable to invest in, and received the lowest scores.
Denandbil is the highest scoring loan, and that is also why it was already funded when I took the screenshot. Investors whether they make their own crazy formula or not, can spot a good deal. The next 2 investments were better in comparison, but still had some issues. The one had a riskier borrower with 70% of decent collateral, but the other had a better borrower with 50% of a slightly better collateral. And the last 2 investments, in my opinion, were inadvisable to invest in, and received the lowest scores.
Look for Risk and Reward in all Investing
Whether its stocks, bonds, real estate, cryptocurrency, or P2P Bitcoin loans. No investor has gotten dumber comparing the risk and reward of competing investments and doing some thinking into probabilities of certain events. I can guarantee that whatever you come up with will be wrong in some way, but that doesn’t mean it won’t be useful. And in the process you will become a better investor. The important part of this whole experiment is taking into account many different variables when investing. For example, even the language used when asking for a loan can be analyzed to predict repayment. So don’t be afraid to use whatever resources available and best practices when investing.
Most households have an unsolved Rubik's Cube. You can esily solve it learning a few algorithms.
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://blog.btcpop.co/2019/03/28/calculating-risk-and-reward-on-investments-at-btcpop/