Building machines that can learn from examples, experience, or even from another machines at human level are the main goal of solving AI. That goal in other words is to create a machine that pass the Turing test: when a human is interacting with it, for the human it will not possible to conclude if it he is interacting with a human or a machine [Turing, A.M 1950].
The fundamental algorithms of deep learning were developed in the middle of 20th century. Since them the field was developed as a theory branch of stochastic operations research and computer science, but without any breakthrough application. But, in the last 20 years the synergy between big data sets, specially labeled data, and augmentation of computer power using graphics processor units, those algorithms have been developed in more complex techniques, technologies and reasoning logics enable to achieve several goals as reducing word error rates in speech recognition; cutting the error rate in an image recognition competition [Krizhevsky et al 2012] and beating a human champion at Go [Silver et al 2016]. Andrew Ng, attributes this success because the capacity of deep NN to learn complicate functions correctly, and its performance that grows proportionally to the input data.
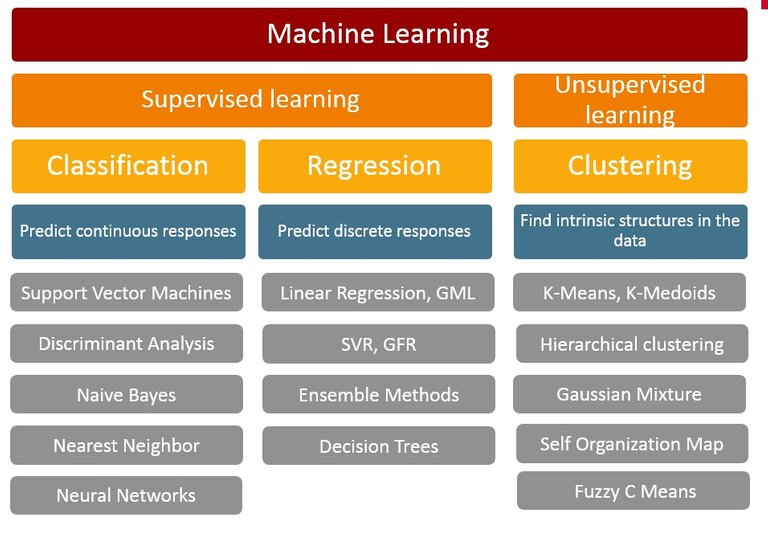
Deep learning is a class of machine learning that allows computational models that are composed of multiple processing layers to learn representations of data with multiple levels of abstraction. [Lecun et al 2015] To understand this technology it is important to know the main techniques of machine learning:
Machine learning techniques are divided in two types: supervised learning, which trains a model that takes known data set (a labeled training set) as input and generates a model that can predict future output of new data. Unsupervised learning takes a dataset (unlabeled) and find patterns or intrinsic structures in data, it usually works as clustering data.
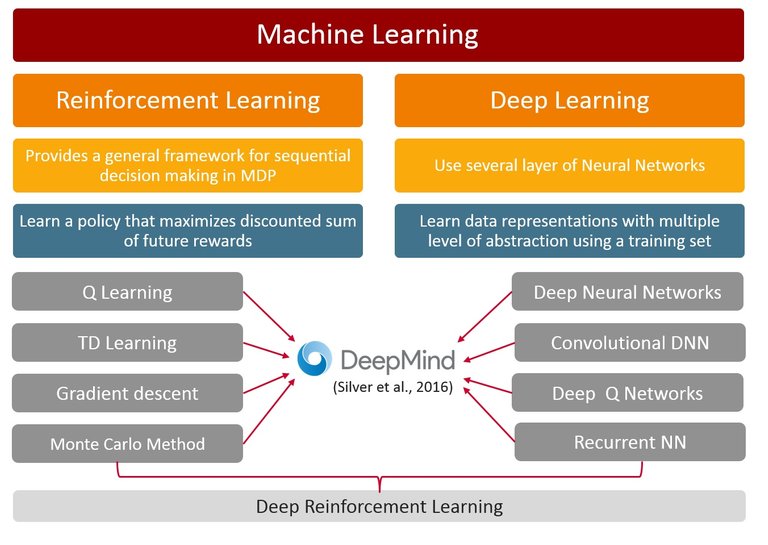
Moreover, reinforcement learning problems involve learning to maximize a numerical reward signal from experience, this is, how to map steps to actions (or create a policy) in order to maximize reward utility. This type of machine learning do not lean from a training set of labeled data, it learns from interaction with its environment. It tries several paths in order to maximize the long term accumulate reward, also call utility. Reinforcement learning is characterized by this points: learning system’s actions influence its later inputs, it doesn’t have direct instructions as to what actions to take, and where the consequences of actions, including reward signals, play out over extended time periods [Sutton & Barto 1998].
Knowledge discovery with efficient algorithms for unsupervised or supervised feature learning
Deep learning is a type of machine learning based in some basic algorithms that were developed in the middle of 20th century. Most of them are used within neural networks, in next section we will show some of the most important algorithms of machine learning.
One of the most powerful techniques in machine learning is Neural Networks because it can be implemented in complementary of different types of machine learning, as show in next sessions. Inspired by the human brain, the neurophysiologist Warren McCulloch and the logician Walter Pits proposed a neural network consists of highly connected networks of functions that map the path from inputs to the desired outputs. It was a fist mathematic approach. The network is trained by iteratively modifying the weights of the connections. [M. Warren, W Piltts 1943]
“Neural networks, with their remarkable ability to derive meaning from complicated or imprecise data, can be used to extract patterns and detect trends that are too complex to be noticed by either humans or other computer techniques. A trained neural network can be thought of as an “expert” in the category of information it has been given to analyze. This expert can then be used to provide projections given new situations of interest and answer what if questions.” [Melin et al 2002]
Also inspired by neurosciences, Rosenblatt [Rosenblatt et al F. 1958] have developed the perceptron, that is an algorithm for learning a binary classifier, it maps the output of each neuron to an 0 or 1; It takes an input vector x, the weigh vector w and evaluate if the scalar product overcome the threshold u, that is f(x) = 1 if wx — u > 0 or 0 otherwise. In simple layer Neural Networks this algorithm wasn’t very useful because binary classification is limited.
In another side, reinforcement learning algorithms were developed from dynamic programing principles. Dynamic programming is the group of algorithms that can solve all type of Markov Decision Process. [Bellman 1957 Dynamic Programing] MDP are mathematical model for modeling decision making in stochastic situation. They are usually represented by a graph, where the nodes are the states and the lines are actions from one state to other, starting from each state each actions have a certain probability to occur independent with the past state or action. Each new state gives a reward (positive or negative). Solve the MDP means to found a policy that maximize the sum of all reward. If the probability to be in a certain state is not 100%, the problem becomes a Partial Observable MDP (POMDP)
Bellman was first in proposing an equation that can solve this problems. [1957 Bellman] this recursive formula provides the utility of following certain policy expecting the highest reward. Solving this equations means finding the optimal policy, this problem was complicate to solve because this equation involves a maximization function, which cannot be derivate. The problem let the domain of reinforcement learning without any relevant advancement until 1989 when Watkins proposed the Q-learning algorithm [Watkins, 1989. Ph.D. thesis] It solve the problem by calculation quantity of state to actions. (SARSA)
Finally the convergence of the solution is warranty by using the Temporal Difference (TD) learning algorithm. It was propose by R. S. Sutton in 1988. [Sutton et al 1988] Since his first used it has become a reference for solving reinforcement learning problems. It ensures the participation of most of the states, helping to solve a challenge born with the exploration-exploitation dilemma.*
Integration of reasoning techniques with deep learning
Deep learning starts when neural networks develop more than just one layer. Working in several layer of neurons was only the first step towards deep learning and data mining. In this section we will expose how the techniques of the first section are integrated into multi-layer neural networks and they developed together the fundaments of deep learning.
Initially the perceptron was conceived to solve one layer neural networks, it works as a one dimension classifier. This technique was not very useful for example in speech or image classification because techniques must be insensitive to irrelevant variations of the input such as orientation of the photo, illumination, zoom, but they should be sensitive to details that difference an image from another (a wolf from a dog for example) .
Perceptron start being useful only in multi-layer networks when Multiple Layer perceptron (MLP) was developed in 1986 by Rumelhart, with a backpropagation technique called Gradient descend. Backpropagation is the ensemble of algorithms aimed to assign the right weights for which the neural network have lower error in its learning. One of the most import methods inside backpropagation is Stochastic Gradient Descent (SGD) this is an algorithm that aims to minimize the error rate using calculus concepts as chain rules for partial derivatives [Rumelhart, et al 1986]. In this technique the derivate of the objective with respect to the input of a neuron can be calculated by computing backwards with respect to the output of that neuron (that’s the input of next neuron) The technique propagate all derives, or gradients, starting from the top output and go all the way to the bottom, then it straightforward compute the respective weight of each link.
Since MLP and SGD, then there was no so much progress in solving neural networks until the proposition of another method of backpropagation called Long Short Term Memory LSTM in 1997 [Hochreiter et al 1997] It shortens the normal gradient descent method an introduces the concept of recurrent network to learn long range dependencies. It leans much faster and solves complex artificial long-time-lag tasks that have never been solved before.
In Deep learning paper LeCun explains the importance its use for the formation of deep learning: “Long short-term memory (LSTM) networks that use special hidden units, the natural behaviour of which is to remember inputs for a long time. A special unit called the memory cell acts like an accumulator or a gated leaky neuron: it has a connection to itself at the next time step that has a weight of one, so it copies its own real-valued state and accumulates the external signal, but this self-connection is multiplicatively gated by another unit that learns to decide when to clear the content of the memory.” [LeCun et al, Nature 2015],LSTM networks let train some type of networks called Recurrent Neural Networks (RNN) that can be train for tasks that involve sequential inputs, such as speech and language [Graves et al 2013]. RNN where the very useful next years, but it didn’t solve the problems of deep learning.
Scientist also developed another type of network that was easier to train, that means, it needs less examples to gain the right weights in the links between neuron, and it also can do better classifications. This network is called Convolutional neural network (CNN) and it is characterized for having a full connectivity between adjacent layers. It appears first in [Lecun et al 1989] with an application of handwritten zip code recognition. The author explain how the convolutional and pooling layers in CNN are directly inspired by the classic notions of cells in visual neuroscience. CNN was the first step in developing computer vision.
Systems combining neural networks and reinforcement learning are the basis of Deep Reinforcement Learning (DRL). In this case the agent in a state use a deep neural network to learn a policy; with this policy the agent takes an action in the environment and gets a reward from the specific state. The reward feeds the neural network and it generates a better policy. This was developed and apply in a famous paper call playing Atari with deep reinforcement learning [Mnih, V. et al 2013] in which they learn a machine to play Atari games directly from pixels, and after training, the machine output excellent results.
Later AlhpaGo team developed a deep reinforcement learning system, using all technologies cited in this session (LSTM, CNN,RNN) creating an artificial intelligence system capable to learn to play the game of Go, be trained watching experts, be trained playing against itself, and finally beating the world champion Lee Sedol. This was a breakthrough in artificial intelligence because due to the complexity of the game, scientist thought it would take more years to make a machine win this game. [Silver et al 2016]
Bibliography
- Bellman, R. (1957). A Markovian decision process (No. P-1066). RAND CORP SANTA MONICA CA.
- Bellman, R. E. (1957). Dynamic programming. Princeton, NJ: Princeton University Press.
- Bottou, L. (2014). From machine learning to machine reasoning. Machine learning, 94 (2), 133–149.
- Ciresan, D., Meier, U., & Schmidhuber, J. (2012). Multi-column Deep Neural Networks for Image Classi cation. In Computer Vision and Pattern Recognition (CVPR) (pp. 3642–3649).
- F. Vernadat, Techniques de modélisation en entreprise : applications aux processus opérationnels, Collection Gestion, Economica, 1999
- GONZALES N. : Contribution à l’amélioration des processus à travers la mesure de la maturité du projet : application à l’automobile, Thèse Doctorale 3 décembre 2009
- Graves, A., Mohamed, A.-r., & Hinton, G. (2013). Speech recognition with deep recurrent neural networks. In Acoustics, speech and signal processing (icassp), 2013 ieee international conference on (pp. 6645–6649).
- Hebb, D. O. (1949). The organization of behavior. Wiley.
- Hinton, G. E., Dayan, P., Frey, B. J., & Neal, R. M. (1995). The \wake-sleep” algorithm for unsupervised neural networks. Science, 268 (5214), 1158–61.
- Juang, B. H., & Rabiner, L. R. (1990). Hidden Markov models for speech recognition. Technometric, 33 (3), 251–272.
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25 (pp. 1097–1105).
- LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521 , 436–444.
- LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard, R. E., Hubbard, W., & Jackel, L. D. (1989). Backpropagation applied to handwritten zip code recognition. Neural Computation, 1 , 541–551.
- LeCun, Y., Bottou, L., Bengio, Y., & H
ner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86 (11), 2278–2323 - Littman, M. L. (1994). Markov games as a framework for multi-agent reinforcement learning. In Proceedings of the eleventh international conference on machine learning (Vol. 157, pp. 157–163).
- McCulloch, Warren; Walter Pitts (1943). “A Logical Calculus of Ideas Immanent in Nervous Activity”. Bulletin of Mathematical Biophysics. 5 (4): 115–133.
- McCulloch, Warren; Walter Pitts (1943). “A Logical Calculus of Ideas Immanent in Nervous Activity”. Bulletin of Mathematical Biophysics. 5 (4): 115–133.
- Melin, P., Castillo, O.: Modelling, Simulation and Control of Non-Linear Dynamical Systems. Taylor and Francis, London (2002)
- Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
- Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychological Review, 65 , 386–408.
- Rumelhart, D. E., Hinton, G., & Williams, R. (1986). Learning representations by back-propagating errors. Nature, 323 (9), 533{536.
- S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
- Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Driessche, G. V. D., . . . Hassabis, D. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529 (7585), 484–489.
- Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Mach. Learn., 39.
- Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction (Vol. 1, №1). Cambridge: MIT press.
- Watkins, C.J.C.H., (1989), Learning from Delayed Rewards. Ph.D. thesis, Cambridge University.
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://towardsdatascience.com/from-classic-ai-techniques-to-deep-learning-753d20cf8578
Hey come and give a shot and see how much you know about deep-learning by explaining the joke and at the same time promote learning AI.