
El arte nace del intento de los humanos de expresarse sobre la experiencia de la vida. El arte puede tomar la forma de escritura, pintura y escultura, así como una variedad de otras formas de expresión. Hay arte en la combinación de función y estética en objetos cotidianos como platos, cubiertos y lámparas. Los matemáticos han podido ayudar a los artistas creando "herramientas" de diversa índole para ellos. Tales herramientas a veces consisten en teoremas que muestran las limitaciones de lo que los artistas pueden hacer. No se puede intentar representar más de 5 poliedros convexos regulares en el espacio tridimensional euclidiano porque las matemáticas muestran que solo hay 5 de estos sólidos regulares. Dodecahedra se puede usar para poner un mes de calendario en cada cara, pero el número de caras de un poliedro convexo regular en 3 espacios euclidianos es 4, 6, 8, 12 o 20. No puede haber otros.
Un tema mucho más importante es el realismo con el que los artistas pueden dibujar en un papel plano lo que perciben cuando observan su mundo tridimensional. Si uno mira los intentos de representación de escenas en arte egipcio y mesopotámico, uno ve que los fenómenos que están asociados con el sistema de visión humana no siempre son respetados. Todos estamos familiarizados con el hecho de que los objetos que están lejos de nosotros parecen más pequeños de lo que realmente son y que las líneas que son paralelas parecen converger en la distancia. Estas características, que son una parte estándar de la forma en que los objetos tridimensionales ahora se representan normalmente en una superficie plana, no se entendieron del todo antes del Renacimiento. Es común referirse a los artistas que usan "perspectiva" (o "perspectiva lineal") para aumentar el realismo de sus representaciones. Los problemas e ideas involucrados en la comprensión de la perspectiva son bastante sutiles y evolucionaron durante un largo tiempo.
La interacción entre académicos y profesionales con respecto a las ideas sobre la perspectiva es paralela a las interacciones entre la teoría y la aplicación que ocurre en todos los ámbitos donde las ideas matemáticas se ponen a trabajar. Un artista puede querer resolver un problema mejor que lo que hizo en el pasado y no siempre se preocupará por las sutilezas de probar que la técnica utilizada siempre funciona o tiene las propiedades que el artista desea. Una analogía para una situación más moderna es que si el sistema actual utilizado para enrutar paquetes de correo electrónico tarda en promedio 7.2 unidades de tiempo y uno descubre una forma de enrutar en 6.5 unidades de tiempo en promedio, uno no debe preocuparse de que uno pueda probar que el mejor sistema haría el trabajo en 6.487 unidades de tiempo.
Las preguntas sobre perspectiva tienen mucho que ver con el espíritu de las preguntas de modelado matemático, ya que en el enfoque habitual nos ocupamos de la percepción de, por ejemplo, una escena en un espacio tridimensional sobre un lienzo plano bajo la suposición de que la escena es siendo visto por un "ojo de un solo punto". Sin embargo, ¡todos sabemos que los humanos están dotados de visión binocular! Estamos atacando estas preguntas de visión binocular hoy, porque tenemos las herramientas matemáticas para hacer esas preguntas, mientras que los artistas / matemáticos del pasado tuvieron que contentarse con enfoques más simples.
Una variedad de personas cuyos nombres son conocidos por los matemáticos (pero quizás no para el público en general) han contribuido a una teoría de la perspectiva. Aunque todos los estudiantes de cálculo conocen el nombre de Brook Taylor (1685-1731)

por su trabajo en series de poder, ¿cuántos matemáticos saben que Taylor escribió sobre la teoría de la perspectiva lineal? Por otro lado, cada historiador de arte reconocerá el nombre de Piero della Francesca (c. 1412-1492), sin embargo, ¿cuántos de estos historiadores del arte (o matemáticos) estarán familiarizados con su contribución a las matemáticas? De manera similar, Girard Desargues (1591-1661) es un nombre bien conocido para los geómetras por su trabajo sobre la geometría proyectiva (en geometría proyectiva plana no hay líneas paralelas), pero pocas personas involucradas en el arte están familiarizadas con su trabajo. El siguiente diagrama (una parte de una "Configuración de Desargues"), familiar para los estudiantes de geometría proyectiva, puede considerarse como un dibujo plano de un punto de "ojo" que ve triángulos que se encuentran en diferentes planos.

Otro colaborador de la teoría de la perspectiva fue Johann Lambert, también conocido por haber producido resultados que se derivarían de suponer que el quinto postulado de Euclides no es válido. Aunque la perspectiva es un área bien minada, esto no detiene el flujo de pensamientos continuados sobre el tema. <span title="For those accustomed to work on one-point or two-point perspective, there is the monograph of D. Termes who treats one- through six-point perspective!
">Para quienes están acostumbrados a trabajar en una perspectiva de un punto o dos puntos, ¡está la monografía de D. Termes que trata una perspectiva de uno a seis puntos!
En relación con la herramienta de perspectiva lineal, se encuentra la rama de la geometría conocida como geometría descriptiva. Si bien la geometría descriptiva se enseñó ampliamente en el siglo XIX, especialmente en las escuelas de ingeniería, el tema no es ampliamente conocido en la actualidad. La razón, en parte, es que el software de computadora hace posible que las personas que no están familiarizadas con la geometría descriptiva realicen tareas que hacen que el conocimiento explícito de la misma sea cada vez más obsoleto. La geometría descriptiva proporciona un conjunto de procedimientos para representar objetos tridimensionales en dos dimensiones. La representación bidimensional puede estar en una hoja de papel o en una pantalla de computadora. Estas técnicas son de gran importancia para los ingenieros, arquitectos y diseñadores. El diseño de, por ejemplo, un avión grande puede implicar decenas de miles de dibujos. Las raíces del tema se encuentran en personas como Albrecht Dürer (1471-1528) y Gaspard Monge (1746-1818). Si un artista, diseñador creativo, escultor o arquitecto no puede entender su concepción de cómo fabricar o ensamblar un diseño "creativo", entonces el trabajo involucrado podría no realizarse. <span title="Descriptive geometry supports both constructive manufacture and creative design by giving procedures for showing how to represent proposed 3-dimensional creations on a flat surface.
">La geometría descriptiva admite tanto la fabricación constructiva como el diseño creativo al proporcionar procedimientos para mostrar cómo representar las creaciones tridimensionales propuestas sobre una superficie plana.
Para dar un poco del sabor de los problemas involucrados, el siguiente diagrama muestra en azul cómo las líneas paralelas "proyectan un triángulo sobre una línea", mientras que las líneas rojas muestran cómo el mismo triángulo se "proyecta" desde el "ojo" hacia el mismo línea:
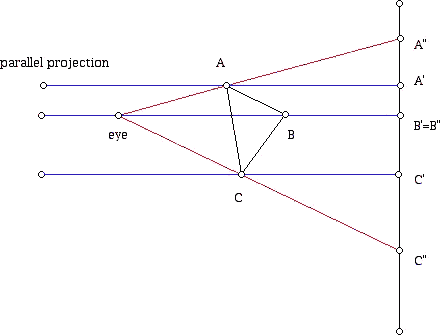
A ', B' y C 'muestran dónde se mueven los vértices mediante proyección "paralela" y A' ', B' 'y C' 'muestran dónde se mueven los vértices mediante proyección "cónica".
Aquí hay un resultado bastante lindo que surgió de esta interacción entre las matemáticas y las necesidades de los artistas para representar tres dimensiones en un plano plano. El resultado se conoce como Teorema de Pohlke. Karl Wilhelm Pohlke (1810-1876) fue un pintor alemán y profesor de geometría descriptiva en una escuela de arte. Formuló este resultado en 1853, aunque la primera prueba parece deberse a K.H.A. Schwarz (1843-1921) en 1864. El teorema se cita en varios niveles de generalidad. Aquí hay una versión:
Teorema (Pohlke): dados tres segmentos (no dos colineales) de longitud especificada (no necesariamente la misma) que se encuentran en un punto en un plano, hay tres segmentos de línea de igual longitud que se encuentran en ángulo recto en un punto en 3 dimensiones espacio tal que una proyección paralela de estos segmentos los mapea en los tres segmentos de línea elegidos en el plano.
Intuitivamente, esto significa que si uno quiere dibujar una caja cúbica en el plano, se puede dibujar cualquier tríada de líneas para una esquina del cubo porque hay una posición de un cubo en 3 espacios que se correlaciona con la tríada dada. Por lo tanto, en el siguiente diagrama, la tríada de la izquierda puede completarse para formar un "cubo", y hay un conjunto de tres segmentos ortogonales en 3 espacios que se pueden mapear mediante proyección paralela en la tríada de la izquierda.

A veces, el Teorema de Pohlke se conoce como el Teorema Fundamental de la Axonometría. La axonometría, al igual que la geometría descriptiva, trata el problema de dibujar objetos tridimensionales en el plano. Aquí hay un artículo reciente coautor por Roger Penrose en este espíritu.
Posted from my blog with SteemPress : https://matematicapositiva.com.ve/matematicas-y-arte-2-herramientas-matematicas-para-artistas/
Congratulations @joseromerogc! You have received a personal award!
Click on the badge to view your Board of Honor.
Do not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Home stretch to the finals. Do not miss them!
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
Saludos... @worksinsane me recomendó tu post... excelente, de lo mejor que he leído en cuanto a ciencia y arte... hay que leerlo varias veces... (Solo una sugerencia: pendiente de incluir la fuente de las imágenes, y no estaría de más incluir referencias para ampliar los temas)...
Congratulations @joseromerogc! You have received a personal award!
Click on the badge to view your Board of Honor.
Do not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - The results, the winners and the prizes