Liebe Steemianer,
im Folgenden anhand konkreter Beispiele ein paar grundlegende statistische Konzepte und Tricks der Statistik, mit denen Aussagen zurechtgebogen werden, sowie auch Tipps, wie Ihr Lügen mit Zahlen besser erkennen könnt. Ich versuche dabei, weitgehend ohne Mathematik auszukommen. Die Mathematiker und Statistiker unter Euch bitte ich um Nachsicht oder eventuell Korrekturen.

Dieses Zitat stammt übrigens gar nicht von Churchill! Quelle
Die Illusion der Präzision
Als am 6.April 1909 der Amerikaner Robert E. Pearyals erster Mensch den Nordpol erreicht hat, war er sich gar nicht sicher, ob er ihn erreicht hatte. Er gab seine Position mit 89 Grad, 57 Minuten und 11 Sekunden nördliche Breite an – eine unglaublich präzise Messung (auf 30m genau!). Selbst heute wäre eine so genaue Messung ein Meisterstück, geschweige denn vor hundert Jahren (1). Damals hätte man die Position bestenfalls auf +-10 km bestimmen können. Er hatte sich die restlichen Stellen einfach ausgedacht, um den Anschein zu erwecken, dort gewesen zu sein. Auch andere Indizien belegen, dass er gar nicht dort war (2).
Praktisches Beispiel Steuerausgleich: Du hast Bücher im Wert von ca. 80€ ausgegeben, die Du absetzen willst, aber dummerweise die Belege verschlampt? Gib´ einfach 78,96€ an. Die Wahrscheinlichkeit, dass keine weiteren Nachweise nachgefragt werden, ist hier viel höher, als wenn Du angibst „ca. 80€“. Die genaue Zahl täuscht Exaktheit vor. Der Trick ist so alt wie die Bibel. Methusalem wurde nicht ca. 1000 Jahre alt, sondern genau 969 Jahre!
Manche Zahlen werden erst durch diverse Rechenoperationen pseudogenau, wie bei dem Bibelschüler, der auf die Frage nach dem Alter der Erde antwortet: „4000 Jahre und eine Woche!“. Als man ihn fragt, woher er das so genau weiß, sagt er: „Na ja, letzte Woche haben wir das gelernt, und da war die Erde 4000 Jahre alt“
Oder diese Vermögensaufstellung:
Haus: € 500.000,-
Bargeld: € 2.345,51
Summe: € 502.345,51
Wenn wir annehmen, dass die Schätzung des Hauswerts nur +-50.000€ genau ist, kann die Summe nicht genauer sein. Welchen Sinn hat es daher, sie auf Cent genau anzugeben? Typischer Fall von Pseudopräzision.
Ähnlich bei vielen statistischen Angaben wie etwa, dass ein Reisbauer in Bangladesch pro Jahr 44,06 € verdient. Höchstwahrscheinlich wurde einfach das geschätzte Volkseinkommen auf die Bevölkerungszahl umgelegt, nach dem Motto „grob rein -> fein raus“. Auch wenn es heißt „102 Kilogramm Rind, Schwein, Geflügel und Fisch ißt der durchschnittliche Österreicher im Jahr“ (3), wird meist davon ausgegangen, dass Verkauf = Konsum ist, doch ist die (unbekannte) Menge an Fleisch, die weggeworfen oder an Haustiere verfüttert wird, sicher nicht zu unterschätzen.
Fazit:
Nie beeindrucken lassen von scheinbar präzisen Daten, sondern immer hinterfragen, worauf sich die Daten stützen!
Die betrügerische Basis
Ein vereinfachtes Beispiel: Ein Einzelhändler kauft Ware um 100€ ein und verkauf sie um 200€. Der Kunde sagt „Unverschämt, 100% Aufschlag!“, der Händler sagt „50% Verdienst ist nicht so viel“.
Beide haben recht, die 100€ Gewinn sind 100% von 100€ und 50% von 200€!
Ein und dieselbe Sache kann also sehr verschieden aussehen, je nachdem, welche Basis man hat oder womit man sie vergleicht.
In Datenvisualisierungen werden gerne die Ausschnitte so gewählt, dass sie zur beabsichtigten Aussage passen, wie hier:
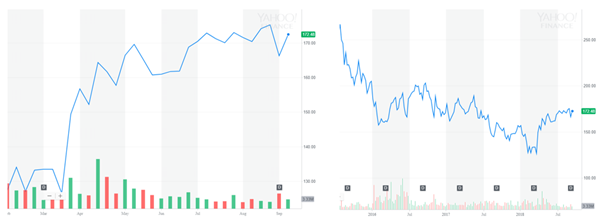
Quelle
Der CEO der Firma X wird vermutlich eher den linken chart nehmen, um den positiven Verlauf der Aktie seiner Firma (seit Feb. 2018) herauszustreichen, ein Aufsichtsratsmitglied, das ihn loswerden will, wird eher den rechten chart verwenden, der den Verlauf seit Juli 2016 zeigt und in dem sich der letzte Aufschwung relativiert. Beide haben recht, der Kontext macht es aus!
Eine falsche Datenbasis nimmt auch der an, der behauptet, alte Menschen seien glücklicher, weil bei Jugendlichen unter 20 der Anteil der Selbstmorde an allen Todesfällen mit 25% am größten ist, und je älter man wird, desto geringer dieser Prozentsatz wird, bis unter 2% bei über 70-Jährigen. In Wahrheit ist es genau umgekehrt und je älter, desto selbstmordgefährdeter (das war schon immer so und ist auch in allen Ländern zu beobachten). Denn dass die Selbstmorde bei Jugendlichen solch eine prominente Rolle spielen, liegt einfach daran, dass Jugendliche generell seltener sterben. Neben Unfällen, Mord und Selbstmord gibt es nur wenige Erkrankungen, die Jugendliche dahinraffen, ganz im Gegensatz zu Alten, die wesentlich häufiger an Krebs, kardiovaskulären und andere Erkrankungen sterben, sodass pro 100.000 70-Jährigen über 50 Selbstmord begehen, bei den unter 20-Jährigen pro 100.000 im gleichen Zeitraum aber nur unter 5. Kann man angesichts dessen immer noch behaupten, Alte seien glücklicher?
Es wäre genauso falsch wie zu behaupten, Autofahren am Tag sei gefährlicher als nachts (weil ja 70% der Unfälle tagsüber passieren) oder dass schnelles Fahren nicht gefährlich sei (weil ja die meisten Unfälle bei moderaten Geschwindigkeiten passieren). Mit Tempo 200 fahren nur sehr wenige, daher kann es hier auch nur wenige Unfälle geben. Bei all diesen Vergleichen darf man aber nur gleich großen Populationen heranziehen und bei diesen die Ereignisrate vergleichen (also Unfälle pro mit 200km/h gefahrene Kilometer vs. Unfälle pro mit 50km/h gefahrene Kilometer).
Sonst müssten auch Krankenhäuser heute die gefährlichsten Orte sein, da heutzutage die meisten Menschen dort sterben (5).
Fazit:
Immer überprüfen, was die Basis ist und ob bei vergleichenden Zahlen die gleichen Grundgesamtheiten herangezogen wurden.
So täuscht man das Auge
Wir alle kennen Umsatzdiagramme, die alle meist von links unten nach rechts oben gehen. Wie schaffen es alle Firmen, ihre Kennzahlen in Prospekten und Präsentationen immer so toll aussehen zu lassen? Indem sie tricksen! Hier das grundlegende Prinzip:
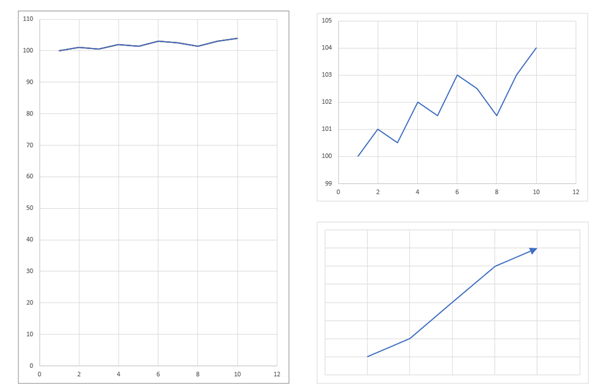
In den drei Diagrammen wurden jeweils die gleichen Zahlen verwendet (100; 101; 100,5; 102; 101,5; 103; 102,5; 101,5; 103; 104). Im linken die ungeschminkte Wahrheit (langweilig), im rechten oberen wurde die senkrechte (y)-Achse einfach gedehnt und die leeren Teile (die aber wichtig für den Gesamtüberblick wären) kurzerhand entfernt. Im rechten unteren Diagramm ist man noch einen Schritt weiter gegangen. Der störende Ausreißer nach unten bei „8“ wurde einfach entfernt, indem man jede 2. Zahl gelöscht hat, die Achsenbeschriftungen wurden weggelassen, dafür ein Pfeil eingefügt, der suggerieren soll, in welche Richtung es weitergehen wird.
Sieht doch schon um einiges besser aus als die ursprüngliche Graphik!
Zusätzlich schneidet man die Kurve links ab je nachdem wie es passt, wie im 1. Kapitel beschrieben.
Achsen können auch logarithmisch formatiert sein und auch die waagrechte (x)-Achse kann problemlos gestreckt werden, sogar nur einseitig. Der Phantasie sind keine Grenzen gesetzt, aber das würde hier zu weit führen.
Fazit:
Bei jedem Diagramm als erstes auf die Achsen schauen. Geben diese keinen Aufschluss oder gibt es keine Beschriftung der Achsen, ist das Diagramm die Zeit nicht wert, es anzusehen.
Prozente
Prozentangaben sind im heutigen Leben allgegenwärtig. Umso erschreckender, dass viele Leute gar nicht wissen, was sie bedeuten! Auf die Frage „Wieviel sind 40%“ antworteten die Hälfte der befragten Bankkunden „einer von 40“ oder „ein Viertel“ (1).
Dabei sind Prozentangaben extrem wichtig, gerade auch bei Wahlen. Wenn eine Partei 24.000 Wahlstimmen erhalten hat, kann das in einer Kleinstadt beachtlich, in einem Bundesland mit ½ Mio Einwohnern immerhin noch 4,8%, aber in einer Nationalratswahl fast nichts mehr sein.
Aber man darf nicht vergessen, jede %-Angabe bedeutet auch Informationsverlust: Vorher hatte man einen Zähler und einen Nenner (z.B. 24.000 von 500.000), danach nur mehr eine Zahl (4,8). Es kann also vorteilhaft sein, nur die Prozentzahl anzugeben, wenn man etwas verschweigen will.
Zum Beispiel könnte ein Parteisprecher großspurig sagen „Wir haben den Anteil der weiblichen Abgeordneten um 50% erhöht“, wenn es in Wirklichkeit jetzt 6 statt vorher 4 sind. Dieses Verstecken kleiner Zahlen hinter Prozenten gilt auch bei diesem Landwirt, dessen Viehbestand aus 57% Kühen, 14% Schweinen und 29% sonstigem Vieh besteht – in echt sind es 4 Kühe, 2 Schafe und ein Schwein.
Bei den verdächtigen Prozentsätzen 33,3 und 66,6 hat die Basis vermutlich (bis zum Beweis des Gegenteils) nur 3!
Mit Prozenten lassen sich auch die flachsten Umsatzverläufe beschönigen. Wenn wir die 3 Umsatzzahlen 100, 101, 102,5 betrachten, so ist das Wachstum im ersten Jahr 1% und im 2.Jahr 1,5/101 = 1,49%, also relativ bescheiden. Wenn man aber die Wachstumsraten der Wachstumsraten heranzieht, so wächst das Umsatzwachstum um stolze 49%! Diese Abstraktion dient rein der Manipulation und hat nichts mit der aktuellen Datenlage zu tun.
Außerdem werden oft Prozente und Prozentpunkte durcheinandergebracht. Wenn eine Partei bei der vorigen Wahl 10% der Wahlstimmen hatte und jetzt 12%, dann hat sie 2%-Punkte dazugewonnen. Im Alltag wird aber oft gesagt, sie hätte 2% gewonnen. Tatsächlich hat sie aber jetzt 20% mehr Wähler hinter sich als bei der letzten Wahl!
Fazit:
Besondere Vorsicht bei Prozentangaben: Warum werden Prozente und nicht absolute Zahlen angegeben, sind Prozent oder Prozentpunkte gemeint? Nicht beeindrucken lassen vom Wachstum der Wachstumsraten und ähnlichen Spielereien.
Mittelwerte
Einen Mittelwert bzw. genauer, das arithmetische Mittel zu bilden, ist sehr praktisch, weil es rasch zu errechnen ist, große Datenmengen verdichten und einen raschen Überblick verschaffen kann. Wenn ein Bauer 3 Kühe hat und der andere 4, hat im Schnitt jeder vier. So weit, so gut.
Leider werden durch diese Art der Mittelwertbildung grobe Ungleichheiten oft verschleiert. Wenn es im Dorf mit 10 Bauern einen gibt, der 40 Kühe hat und die anderen keine einzige, hat im Schnitt trotzdem jeder vier. Daher wäre man gut beraten, bei Verdacht auf Schieflage eine andere Art des Mittelwerts, den Median zu ermitteln. Beim Medien sind die Hälfte der Werte kleiner und die andere Hälfte der Werte größer als der Median. Bei den Schulnoten 1,3,5,4,4,5,2 ist das arithmetische Mittel (1+3+5+4+4+5+2)/7 = 3,4. Der Median ist aber 4 (der mittlerste Wert, wenn alle Werte der Größe nach geordnet werden: 1,2,3,4,4,5,5). Ein anderer Vorteil des Medians ist, dass immer ein realer Wert entsteht (real nicht im math. Sinn, sondern es ist ein Wert gemeint, den es im echten Leben geben kann, also nicht „im Schnitt 1,5 Kinder pro Frau“). Der Median im Dorfbeispiel ergibt 0 und die starke Diskrepanz zum arithmetischen Mittel 4, zeigt auf, dass es hier eine „schiefe Verteilung“ gibt. In diesem Fall rechts-schief (wenn es viele kleine, aber nur wenige große Werte gibt), was häufig bei Einkommensverteilungen auftritt. Der Oberbauer mit seinen 10 Kühen zieht das arithmetische Mittel „zu sich“, während der Median robust gegen solche Ausreißer ist.
Wer also Werte gerne kleiner hätte als sie sind, kann einfach die Art des Mittelwerts wechseln - der Durchschnittsleser wird es kaum bemerken. Das Durchschnittsgehalt der Ärzte wird von der Ärztekammer sicher lieber im Median angegeben.
Leider reicht der einfache Mittelwert nicht immer. Ein Imbißbudenbesitzer wurde mal gefragt, woraus sein „Wildragout-Burger“ bestehe. Er gab an, dass auch Pferdefleisch drin sei. Auf die Frage wieviel Pferdefleisch, antwortete er „Halb und halb, ein Pferd und ein Kaninchen.“ Beim arithmetischen Mittel sind alle Werte gleich, de facto bestehen diese Burgern aber fast nur aus Pferdefleisch.
Wenn in einer Firma die Frauen 8€ pro Stunde verdienen, die Männer aber 12€, ist der Durchschnittslohn nur dann genau 10€, wenn gleich viele Männer und Frauen dort beschäftigt sind. Ist der Frauenanteil >50%, verschiebt sich der Durchschnittslohn nach unten. Für den korrekten Durchschnittslohn muss man „gewichten“, d.h. bei 70% Männern und 30% Frauen ist der gewichtete Durchschnitt 0,7x12 + 0,3x8 = 10,8€. Wie man gewichtet, ist leider nicht immer so einleuchtend wie in diesem Beispiel.
Ein gewichteter Durchschnitt wird auch bei der Inflationsberechnung verwendet, beim Preisindex für die Lebenshaltung. Die aktuellen Preise der Güter im sog. Warenkorb(6) werden geteilt durch die Preise in der Basisperiode und diese dann mittels eines gewichteten arithmetischen Mittels zum Preisindex kondensiert. Das Problem ist hier aber, wie die Gewichtung errechnet wird, denn abhängig von der Preissteigerung können bestimmte Guter entsprechend weniger stark nachgefragt werden (elastische Nachfrage), sodass die Gewichtung ständig angepasst werden muss.
Auch bei der Bestimmung des Mittelwertes spielt es eine wesentliche Rolle, welche Basis herangezogen wird: Welches Verkehrsmittel ist sicherer, die Bahn oder das Flugzeug? Die Antwort ist verschieden, je nachdem welche Basis man nimmt:
- Bahn: 9 Todesfälle pro 10 Mrd Passagierkilometer
- Flugzeug: 3 Todesfälle pro 10 Mrd Passagierkilometer
Wenn das stimmt, Flugzeuge also 3x so sicher sind, wieso haben dann so viele Menschen Flugangst und so wenige Bahnangst? Alles irrational?
Wenn man statt der zurückgelegten Kilometer die verbrachten Stunden in dem Verkehrsmittel berücksichtigt, sieht die Sache ganz anders aus.
- Bahn: 7 Todesfälle pro 100 Mio Passagier-Stunden
- Flugzeug: 24 Todesfälle pro 100 Mio Passagier-Stunden (1)
Meiner Meinung nach ist die zweite Berechnung korrekter, da ich mich auch ohne Bedenken jeden Tag in ein Bett lege, obwohl die Wahrscheinlichkeit in einem solchen zu sterben bei 99% liegt!
Fazit:
Beachte immer, welchen Mittelwert man warum verwendet hat, ob korrekt gewichtet wurde und ob die Basis sinnvoll ist!
In Teil II dann mehr über Stichproben und Korrelation vs. Kausalität!
Quellen/Anm.:
(1) Walter Krämer, „So lügt man mit Statistik“, Piper Verlag München (2000)
(2) https://de.wikipedia.org/wiki/Geschichte_der_Nordpolexpeditionen#Amerikanische_Expeditionen
(3) https://diepresse.com/home/wirtschaft/economist/5272939/Wir-essen-mehr-Fleisch-denn-je
(4) https://staatsschulden.at/
(5) In diesem Fall würde ich aber eine Ausnahme machen, denn ich halte Krankenhäuser tatsächlich für gefährliche Orte, da dort oft unangenehme, multiresistente „Spitalskeime“ die behandelten Patienten infizieren können (nosokomiale Infektionen), doch das ist eine andere Geschichte…
(6) https://de.wikipedia.org/wiki/Warenkorb
ine-split-tests/#i.1cx22l711y5eul)
Wirklich gut beschrieben, überhaupt mit dem Flugzeug und der Bahn, ein Parameter wird geändert und das Ergebniss ist aufeinmal Posetiv.
Auf die Frage „Wieviel sind 40%“ antworteten die Hälfte der befragten Bankkunden „einer von 40“ oder „ein Viertel“ (1).
Wie viele befragt, wo, Grundgesamtheit, Repräsentativität :P.
Ist schon ein interessanter Professor der Krämer.
Danke für die Aufarbeitung, top!
Haha, erwischt :)
dem Geiste der Ratschläge und Fazite im Text gefolgt :)
so sollte es ja sein :D
Genau, war in Wirklichkeit natürlich ein eingebauter Test :)
Großartig!
Wieder was zum Archivieren.
Unglaublich spannend zum lesen. Da mir gewisse Tricks schon bekannt waren, hab ich doch den einen oder anderen noch entdeckt auf den ich nächstes mal achten werde.
Vielen Dank für diese spannende Abendlektüre.
so wird es gefälscht
und mit Aussagen zu Wahrscheinlichkeitsverteilungen wo sie keinen Sinn machen oder der Wahl des Samples wird es schließlich ad absurdum geführt. BIP, BSP, wo es allen blendend geht, wo alle Leistungsträger sind, wo die meisten beschäfftigt sind.
:D:D:D orginal unser Dönermann mit ernster osmanischer Miene
resteem das mal, war ja wirklich viel und gute Arbeit.
Servus,
du hast von mir ein Upvote erhalten! Ich bin ein Curation-Bot und meine Mission ist, hochwertigen Content unter #steemit-austria zu fördern. Hier kannst du mehr über mich und meine Funktionsweise erfahren. Wie du an meinen Curation-Rewards mitverdienen kannst, wird dort ebenfalls beschrieben.
Übrigens: Wenn du den Tag #steemit-austria verwendest, finde ich deine Posts noch leichter!
Auf dem dem Steemit-Austria Discord-Server kannst du nette Leute kennen lernen und deine Beiträge promoten.
Zum aktuellen Tagesreport
Servus,
du hast von mir ein Upvote erhalten! Ich bin ein Curation-Bot und meine Mission ist, hochwertigen Content unter #steemit-austria zu fördern. Hier kannst du mehr über mich und meine Funktionsweise erfahren. Wie du an meinen Curation-Rewards mitverdienen kannst, wird dort ebenfalls beschrieben.
Übrigens: Wenn du den Tag #steemit-austria verwendest, finde ich deine Posts noch leichter!
Auf dem dem Steemit-Austria Discord-Server kannst du nette Leute kennen lernen und deine Beiträge promoten.
Zum aktuellen Tagesreport
Danke für den Einblick in ein sehr interessantes Thema. Hat Spaß gemacht zu lesen. Vorallem die Bespiele mit dem Diagramm und dem Bahn/Flugzeug vergleich waren sehr interessant.
Hier noch ein Addendum, das mir wieder einfiel:
97% oder 0,3% oder etwas dazwischen?
Kommt auf die Sichtweise auf die Daten an :P
Hi @stayoutoftherz!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 3.224 which ranks you at #8196 across all Steem accounts.
Your rank has improved 8 places in the last three days (old rank 8204).
In our last Algorithmic Curation Round, consisting of 441 contributions, your post is ranked at #122.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server