Et voilà, c’est parti pour mon dernier article de physique de l’année. Je profite actuellement de quelques jours à Bruxelles durant lesquels se mêlent travail et loisirs, avant un retour en France prévu en fin de semaine. Ce séjour en Belgique ne m’a pas empêché d’écrire, comme vous allez pouvoir le voir ci-dessous (on ne va pas parler de longues nuits d’hiver, mais presque). Le sujet du jour concerne le cœur de mes recherches, à savoir les phénomènes au-delà du Modèle Standard de la physique des particules.
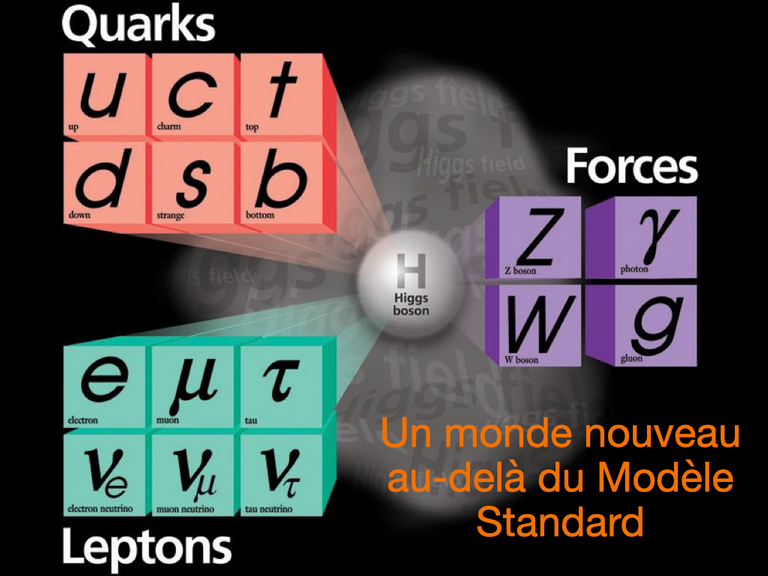
Dans le post d’il y a deux semaines, j’ai détaillé la construction du Modèle Standard particule par particule. Ensuite, le post de la semaine dernière s’est concentré sur l’histoire du boson de Higgs, depuis les motivations théoriques des années 1960 jusqu’à la découverte d’il y a quelques années, avec bien entendu une petite fenêtre sur les possibilités des 100 prochaines années.
Pour résumer, nous avons un cadre théorique couronné de succès divers et variés (i.e. le Modèle Standard), qui fournit non seulement une explication à toutes les données de physique des hautes énergies collectées jusqu’à aujourd’hui, mais aussi des prédictions pour les expériences en cours et à venir. Cependant, cela n’empêche pas ce que les physiciens des hautes énergies appellent la ‘physique au-delà du Modèle Standard’, ou la ‘nouvelle physique’, d’être un domaine de recherche extrêmement actif. Cela concerne de façon générique tous les phénomènes prédits par les théories étendant le Modèle Standard, à la fois du point de vue théorique et dans le contexte de recherches expérimentales (par exemple au Grand Collisionneur de Hadrons au CERN).
Bien entendu, j’ai déjà dit de nombreuses fois que le Modèle Standard marchait super bien. C’est pour cela que nous parlons d’extensions du Modèle Standard. En gros, le Modèle Standard peut être vu comme la partie visible d’un iceberg qu’il nous reste à sonder en profondeur.
Dans ce blog, je vais essayer de mettre en avant plusieurs des raisons qui font que nous espérons observer tout un tas de phénomènes nouveaux dans les prochaines années. Il s’agit des motivations-mêmes de mes propres activités de recherche. Comme il est impossible de parler de toutes les limitations conceptuelles du Modèle Standard, j’ai choisi de me concentrer sur ce que je considère (de façon tout à fait subjective) comme les motivations principales à la physique au-delà du Modèle Standard. Je vais cependant illustrer la diversité de ces limitations en fin de post.
[Crédits: Fermilab]
Les masses des neutrinos
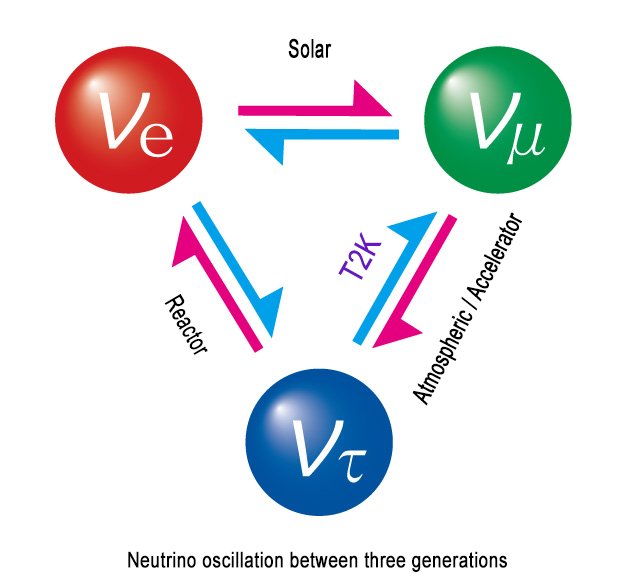
Dans le post d’il y a deux semaines, je me suis concentré sur l’origine du contenu en particules du Modèle Standard. J’ai ainsi indiqué qu’il contenait trois types de neutrinos (le neutrino électronique 𝞶e, le neutrino muonique 𝞶𝝁 et le neutrino tau 𝞶𝜏). Les neutrinos sont les particules les plus furtives connues actuellement. Cela provient de leur nature faiblement interagissante. Les interactions des neutrinos sont en fait tellement faibles que 1,000,000,000,000 neutrinos parviennent à traverser chaque être humain de la planète sans interagir… à chaque seconde !
Cependant, malgré cette nature insaisissable, les neutrinos ont été observés dans de nombreux processus, et certaines de leurs propriétés ont été déterminées de façon assez précise. Jusqu’il y a peu, ces observations corroboraient le fait que les neutrinos sont des particules non massives dans le Modèle Standard. Le seul petit souci est qu’en 2015, il a été démontré que les neutrinos oscillaient lors de leur propagation, c’est-à-dire qu’ils changeaient de type.
Par exemple, si nous préparons un faisceau de neutrinos électroniques à un endroit donné A et l’envoyons vers un autre endroit B, nous observerons que le faisceau en B contiendra surtout des neutrinos électroniques, mais également des neutrinos muoniques et des neutrinos taus qui n’étaient pas là au départ.
[Crédits: J-Parc]
Ces ‘oscillations’ de neutrinos sont un gros problème pour le Modèle Standard, car elles ne sont possibles que si les neutrinos sont non-massifs. Nous avons donc ici un fait (les masses non-nulles des neutrinos) qui découle de l’observation des oscillations de neutrinos, et qui contredit le Modèle Standard. Ce dernier a en effet été bâti en accord avec d’autres propriétés, observées il y a plus longtemps et qui pointaient vers des neutrinos non-massifs.
On pourrait se dire qu’il suffit d’utiliser le boson de Higgs comme pour la modélisation des masses de toutes les autres particules. Mais dans le cadre des neutrinos, cela n’est pas possible. Par conséquent, les neutrinos représentent à mes yeux l’une des meilleures motivations justifiant une extension du Modèle Standard.
Il nous faut généraliser le Modèle Standard afin que les neutrinos y soient massifs. Le meilleur mécanisme permettant cela est appelé le mécanisme seesaw (on va éviter la traduction littérale de ‘balançoire’, qui sonne vraiment bizarrement à mon oreille). Sans entrer dans les détails, ce mécanisme implique l’existence de nouvelles particules.
Par conséquent, la physique des neutrinos concerne une partie non négligeable des recherches au Grand Collisionneur de Hadrons du CERN, avec notamment des possibilités d’observation de nouvelles particules et phénomènes associés. De mon côté, j’ai commencé à plancher sur ce sujet il y a 2 ans. J’écrirai peut-être un article sur mes recherches à ce propos l’année prochaine.
La matière noire
Une autre motivation pour l’étude des extensions du Modèle Standard n’est autre que la célèbre matière noire. Pour comprendre cela, je vais discuter en quelques mots de ce que nous appelons le modèle standard de la cosmologie. Dans ce contexte, l’univers ne contient pas seulement de la matière sous forme visible (‘visible’ dans le sens où la matière émet, réfléchit et/ou absorbe de la lumière), mais aussi de la matière de nature différente de ce que nous connaissons.
De façon plus quantitative, 85% de la matière présente dans l’univers apparaît alors sous forme noire, ou sombre par opposition à visible. Il existe plusieurs raisons qui font que nous sommes (pour la plupart) convaincus de cela. Ces raisons sont cependant toutes indirectes. Je reviendrai sur cette nature indirecte des preuves ci-dessous.
Les origines de la matière noire telle que nous la concevons aujourd’hui proviennent du travail de Zwicky dans les années 1930. Ce dernier étudiait le mouvement de rotation des étoiles dans une galaxie lointaine. En particulier, il a mesuré la vitesse de rotation des étoiles en fonction de leur éloignement du centre de la galaxie. D’un autre côté, cette vitesse peut être calculée à partir des lois de la mécanique classique en prenant en compte le fonctionnement de la gravité et la quantité de matière visible.
Les résultats des calculs et des observations ne collaient cependant pas. Zwicky a alors proposé l’existence de matière invisible, et a refait les calculs en prenant cela en compte. Il a alors obtenu un bon accord entre la théorie et les données.
Cette idée fut confirmée 30-40 années plus tard par Vera Rubin lors de son étude de nombreuses galaxies. Rubin fournit ainsi la première preuve quantitative (mais indirecte) de l’existence de la matière noire. Elle a également confirmé que l’univers contenait surtout de la matière noire (par rapport à la matière visible).

[Crédits: ESA (CC BY-SA IGO 3.0)]
Mais cette histoire de matière noire est loin d’être finie. Il existe de nombreuses autres preuves.
Par exemple, les données liées au fonds diffus cosmologique, telles que celles mesurées par la collaboration Planck, pointent vers le fait que la matière noire est une composante essentielle de l’univers. Pour comprendre cela, commençons par rappeler que le fonds diffus cosmologique n’est autre que le rayonnement fossile témoignant du Big Bang.
Ce rayonnement a une température moyenne de 2.72 degrés Kelvin (ou -270.42 degrés Celsius) et est présent partout dans l’univers. Cependant, une valeur moyenne n’est qu’une valeur moyenne. La température du rayonnement fossile dépend ainsi de la position dans l’univers. Cela est très bien expliqué par la cosmologie standard, pour laquelle la matière noire est essentielle (et réelle).
Un dernier exemple (il y en a d’autres mais je vais m’arrêter après cet exemple) concerne la formation des galaxies au cours de l’évolution de l’univers. Sans matière noire, les simulations de la vie de l’univers ne parviennent par à reproduire l’univers tel qu’il est aujourd’hui.
Nous avons ainsi un très grand nombre de faits qui pointent vers la nécessité de la matière noire. Mais tous ces faits sont indirects. Il nous manque encore une observation directe de matière noire. Cette dernière peut s’obtenir de deux façons : soit via les expériences attendant patiemment qu’une particule de matière noire entre en collision avec un détecteur placé dans un endroit calme de la planète (comme par exemple l’expérience Xenon1t en Italie), soit aux collisionneurs (tels que le Grand Collisionneur de Hadrons du CERN).
Revenons à présent au Modèle Standard. Ici c’est simple : aucune particule connue ne peut jouer le rôle de matière noire. Il nous faut donc étendre le contenu en particules du Modèle Standard et y incorporer une particule qui serait une bonne candidate pour la matière noire. Cela nous mène automatiquement au concept de théories au-delà du Modèle Standard, et à toute une série de phénomènes nouveaux potentiellement observables.
La problématique de la matière noire est ainsi assez cruciale pour mes recherches, et j’ai co-écrit de nombreuses publications scientifiques à ce sujet. Ce blog contiendra donc naturellement de nombreux posts traitant de la matière noire.
Le problème de la hiérarchie
À présent, je vais discuter non plus d’un problème du Modèle Standard qui vient des données, mais d’un problème conceptuel. Il s’agit de ce qui est appelé le problème de la hiérarchie.
Son nom vient du fait que nous avons une importante différence entre les ordres de grandeur de deux quantités. Ces quantités sont les échelles d’énergie pertinentes pour le Modèle Standard. Pour la suite de la discussion, je rappelle qu’en physique des particules, masses et énergies sont exprimées en GeV, où 1 GeV est égal à la masse du proton (c’est-à-dire la masse d’un noyau d’hydrogène).
La première échelle d’énergie dont nous parlons est reliée à la masse des bosons W et Z. Ces deux masses sont approximativement les mêmes et valent environ 100 GeV. C’est ce qui est appelé communément l’échelle électrofaible. J’en profite pour introduire au passage un peu de vocabulaire. La ‘théorie électrofaible’ est le cadre théorique dans lequel l’électromagnétisme et les interactions faibles sont unifiés.
La seconde échelle d’énergie pertinente pour le Modèle Standard est l’échelle de Planck, qui est égale à 1019 GeV (ou 10,000,000,000,000,000,000 GeV). Pour de telles énergies, les effets gravitationnels ne peuvent plus être négligés. Le Modèle Standard ne contenant pas la gravité cesse donc d’être valide.
[Crédits: OLCF (CC BY 2.0)]
Nous avons donc deux échelles qui sont très différentes. Cette différence, ou hiérarchie, mène à un problème parfois vu comme un paradoxe. Ce dernier est lié au fait que le Modèle Standard est une théorie quantique.
Cette nature quantique du Modèle Standard fait que toute prédiction d’une grandeur mesurable doit inclure tout un tas de ‘corrections quantiques’. Prenons un exemple concret : la ‘valeur dans le vide du champ de Higgs’. Je ne définirai pas ce qu’est cette quantité. À la place, je me contenterai de dire qu’il s’agit de la grandeur qui contrôle la valeur des masses des bosons W et Z. Autrement dit, la valeur du Higgs dans le vide contrôle l’ordre de grandeur de l’échelle électrofaible (qui est de 100 GeV).
Si on prend en compte les corrections quantiques aux prédictions, cette valeur dans le vide du champ de Higgs devient égale à 10,000,000,000,000,000,000 GeV (il s’agit de l’échelle de Planck). C’est une catastrophe vu que cela rend la théorie totalement incompatible avec les données (on a un résultat qui est 100,000,000,000,000,000 fois trop grand). Cela peut être évité de deux façons.
Tout d’abord, on pourrait fixer la vingtaine de paramètres du Modèle Standard jusqu’à leur trentième décimale. Se faisant, on mettrait en jeu des compensations un peu miraculeuses au niveau des corrections quantiques et on obtiendrait une valeur dans le vide du Higgs de l’ordre de 100 GeV. Mais cette solution n’est vraiment pas terrible. Elle implique que changer la 31ème décimale d’un seul paramètre suffit à renvoyer la valeur dans le vide du Higgs à l’échelle de Planck (et la théorie se re-casse alors la figure). De plus, on aura jamais la précision expérimentale nécessaire pour mesurer les paramètres du Modèle Standard à ce niveau.
Une autre solution à ce problème de hiérarchie, plus satisfaisante, existe cependant. Il suffit de voir le problème de la hiérarchie comme émergeant du fait qu’il existe d’autres blocs de base de la nature, que nous n’avons pas encore découverts (et qui ne sont donc pas inclus dans le Modèle Standard). L’impact de ces nouvelles particules produit alors les compensations désirées au niveau des corrections quantiques. Dans cette optique, le problème de la hiérarchie est simplement lié au fait que le Modèle Standard n’est pas complet.
Cette deuxième solution est bien entendu celle qui est préférée dans la communauté de physique des hautes énergies : le problème de hiérarchie dans le Modèle Standard n’est un problème que parce que seulement une partie de la théorie a été découverte.
La plupart des extensions du Modèle Standard proposant une solution au problème de hiérarchie contiennent généralement un certain nombre de nouvelles particules qu’il nous faut encore découvrir. De plus, le fait que la valeur dans le vide du champ de Higgs doit être de l’ordre de 100 GeV implique que ces nouvelles particules ne doivent pas se trouver trop loin de l’échelle électrofaible.
Ce régime d’énergie étant celui sondé au Grand Collisionneur de Hadrons, on s’attend ainsi à observer des nouveaux phénomènes dans les données qui seront collectées dans les prochaines années. Il faut noter qu’au jour d’aujourd’hui, les données sont cependant en très bon accord avec le Modèle Standard, mis à part certaines anomalies intéressantes.
Les échecs du Modèle Standard en tant que motivations pour son extension
Je me suis concentré sur trois des raisons qui motivent l’étude d’extensions du Modèle Standard, à savoir la problématique de la matière noire, la modélisation des masses des neutrinos et le problème de la hiérarchie entre l’échelle électrofaible et l’échelle de Planck. Ces trois raisons sont celles que je considère personnellement comme les plus importantes pour justifier le fait que le Modèle Standard n’est que la partie visible de l’iceberg, pour reprendre l’image du début de post. Il y en a cependant de nombreuses autres. En voici quelques-unes.
- L’unification : dans le Modèle Standard, seulement deux des trois interactions fondamentales sont unifiées (l’électromagnétisme et les interactions faibles). Il nous faut généraliser la théorie pour pouvoir aussi unifier l’interaction forte.
- La gravité : il existe une quatrième interaction fondamentale, la gravité, qui n’est pas prise en compte dans le Modèle Standard. Ce n’est pas un problème en soi car nous savons qu’aux énergies sondées actuellement la gravité n’a pas d’effet. Mais au niveau théorique c’est peu satisfaisant. De plus, nous ne savons pas comment faire cela.
- Trois familles : nous avons trois neutrinos, trois leptons chargés et deux ensembles de trois quarks (trois quarks d’un ensemble donné ayant les mêmes propriétés). Pourquoi trois ?
- Quelle est la nature de l’énergie noire, cette dernière étant nécessaire pour expliquer l’expansion accélérée de l’univers ?
- Où est donc passé l’antimatière ? L’univers d’aujourd’hui est en effet constitué entièrement de matière.
- Pourquoi vivons-nous dans un espace-temps quadri-dimensionnel ? Peut-il y avoir des dimensions supplémentaires ?
Et comme je l’ai dit, cette liste est en fait bien plus longue. Nous avons des dizaines de justifications à une extension du Modèle Standard, de sorte que les physiciens sont assez confiants dans le fait que le Modèle Standard n’est pas une finalité en soi. Ainsi, les recherches liées aux phénomènes au-delà du Modèle Standard sont nombreuses, des dizaines de publications scientifiques apparaissant chaque jour.
Dans ce blog, je me suis concentré sur les trois raisons que je trouve les plus importantes, toutes les raisons mentionnées motivant cependant mon travail de recherche. En tant que physicien théoricien des particules, j’essaie de contribuer avec les moyens qui sont miens à tout un domaine de recherche visant à améliorer notre compréhension de l’univers.
Deux questions (parmi d’autres) m’interpellent tout particulièrement. Qu’est-ce que la physique au-delà du Modèle Standard pourrait être ? Qu’est-ce qu’elle ne pourrait pas être ? Tenter de répondre à ces questions d’une façon ou d’une autre permettent d’apprendre plein de choses, qui pourront potentiellement améliorer notre vision du monde qui nous entoure. Cet aspect-là est assez génial en soi. Chaque jour on en apprend un peu plus !
Sur ce, je vous dis à bientôt, et j’attends avec impatience les questions et commentaires éventuels. Dans tous les cas, je vous souhaite à toutes et tous de joyeuses fêtes de fin d’année, et rendez-vous en 2022 pour un nouvel article de physique des particules ou de cosmologie.
Bonjour bonjour, c'est l'emmerdeur 🤣 J'avais gardé comme d'habitude une question en réserve (bon Ok une double + une subsidiaire).
Le vide n'étant pas vide, particules virtuelles (en passant comme j'ai cru comprendre dans un commentaire que les trous noirs étaient dans ta Wishlist pour un de ces jours j'espère que tu y parleras du rayonnement de Hawking), je voulais savoir si:
peut-il exister un endroit dans l'univers (observable ou non) avec des particules a 0 degré kelvin et donc avec un temps propre arrêté ou est-ce impossible par les lois de la physique et sinon sont-elle "réveillable"?
est-ce que la/les particule composant la matière noire pourrait être comparable aux particules virtuelles au niveau de leur "durée de vie" empêchant ainsi de la/les détecter directement, les effets de la matière noire étant ici issue du fait du très grand nombre de création/désintégration?
Allez une dernière pour la route (d'ailleurs comme d'habitude ne réponds que lorsque tu auras le temps, cela peut très bien attendre):
Normalement, demain c'est le lancement du télescope James Webb depuis Kourou, je sais qu'il va y avoir encore une bonne année avant qu'il soit complètement opérationel mais je voulais savoir, une fois qu'il le sera, est-ce qu'il pourra avoir un impact sur tes recherches ou celle aux CERN? Pas exemple pour confirmer quelque chose ou ouvrir de nouvelles pistes? Par une communication directe avec les personnes en charge du télescope ou via leurs publications?
Mais non ce n'est pas l'emmerdeur! Je serais au contraire surpris si je ne recevais pas de commentaire de ta part. Pour les trous noirs, on verra exactement quand. Une chose est sure est que ca ne sera pas prochainement, car j'ai deja d'autres choses au programme pour janvier (et fevrier en fait).
Je vais a present repondre a tes questions.
Ce que tu proposes est interessant conceptuellement, mais pas en accord avec les donnees. Les fluctuations dans le fonds diffus cosmologique sont de l'ordre de quelques pourmilles. En gros, les temperatures varient entre 2.721 et 2.729 degres Kelvin, pour une valeur moyenne de 2.725 degres Kelvin (il faut trois decimales pour le voir ;) ).
Je recommande cette page pour des infos un peu plus detaillees (et des jolies images). Elle est un peu vieille, et il y manque les resultats les plus recents de Planck. Pour ces derniers, cette page est excellente.
Une particule virtuelle est... virtuelle. C'est-a-dire qu'elle n'est pas reelle. En fait, il faut plutot voir les particules virtuelles comme des artefacts de calcul en theorie des champs quantiques permettant de relier un etat initial donne et un etat final donne. Elles n'ont donc a proprement parler aucune duree de vie specifique, vu que ces dernieres "ne vivent pas" (tu noteras les guillemets).
Une particule, qu'elle soit reelle ou virtuelle, a en effet une duree de vie bien donnee, qui est une de ses proprietes calculables. Cette duree de vie moyenne (j'insiste sur le "moyenne") est associee a la probabilite de survie de la particule apres un temps donne (une particule peut toujours vivre plus longtemps que sa duree de vie moyenne; cela devient juste de plus en plus rare et improbable a mesure que le temps considere augmente.
Le probleme de la detection de la matiere noire est simplement liee a sa nature faiblement interagissante. Cette derniere implique que ces processus sont rares, et donc difficile a observer, que cela soit dans les experiences de detection directe ou au Grand Collisionneur de Hadrons.
Peut-etre que demain finalement, cela aura lieu ;)
En ce qui me concerne, il y a une facette du programme de physique du JWST liee a l'observation de galaxies lointaines qui pourrait concerner mes recherches (qui sont plus "astroparticules" que "cosmologie" ou "astrophysique"). Cela pourrait avoir un impact sur notre comprehension de la physique de la matiere noire et la cosmologie entre l'epoque du Big Bang et celle de la formation des premieres galaxies. Tu trouveras par exemple des infos la-dessus ici.
Mais on parle ici de moyen voire long terme.
Sur ce, a bientot (je me mets en route pour un retour en France).
Merci pour tous ces éclaircissements sur ton champ de recherche.
J'ai une formation scientifique de base plutôt axée maths mais qui commence à dater. J'ai moins poussé en physique alors j'essaie de suivre avec ce qu'il me reste.
Donc en clair :
Vous supposez que la théorie standard est une portion d'une théorie beaucoup plus large.
Cette hypothèse repose sur le fait que la connaissance des différentes particules et de leurs interactions n'est pas en mesure d'expliquer certaines incohérences observées et/ou mesurées.
Par conséquent, il existe forcément d'autres particules qui pourraient lever ces doutes mais on n'est pas en mesure de le prouver formellement ni de les identifier.
En somme, Tout un champ de connaissance à découvrir.
Pour établir un raccourci (grand raccourci) comparatif historico-scientifique, la théorie standard peut être comparée à la relativité galiléenne quand Einstein énonçait les principes de la relativité générale.
Le raccourci est grand, j'avais prévenu.
Votre principale difficulté sera sans doute d'identifier par des mesures tangibles ces particules.
Mais est-on en mesure de créer des appareils de mesures précis et des modèles, je suppose, mathématiques associés quand on ne sait pas trop ce que l'on cherche?
L'évolution de l'informatique quantique peut-elle apporter une aide par sa puissance de calcul ?
@tipu curate
Upvoted 👌 (Mana: 26/66) Liquid rewards.
Merci Marc !
Ho Ho Ho! @lemouth, one of your Hive friends wishes you a Merry Christmas and asked us to give you a new badge!
The HiveBuzz team wish you a Merry Christmas!
May you have good health, abundance and everlasting joy in your life.
To find out who wanted you to receive this special gift, click here!
You can view your badges on your board and compare yourself to others in the Ranking
Check out the last post from @hivebuzz:
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more